5. makemore (part 4): becoming a backprop ninja#
import sys
IN_COLAB = "google.colab" in sys.modules
if IN_COLAB:
print("Cloning repo...")
!git clone --quiet https://github.com/ckaraneen/micrograduate.git > /dev/null
%cd micrograduate
print("Installing requirements...")
!pip install --quiet uv
!uv pip install --system --quiet -r requirements.txt
Intro#
Hi everyone. So today we are once again continuing our implementation of makemore!
Bigram (one character predicts the next one with a lookup table of counts)
MLP, following Bengio et al. 2003
RNN, following Mikolov et al. 2010
LSTM, following Graves et al. 2014
GRU, following Kyunghyun Cho et al. 2014
CNN, following Oord et al., 2016
Transformer, following Vaswani et al. 2017
Now so far, from the above list, we’ve come up to mlps and our nn has looked like this:
from IPython.display import Image, display
display(Image(filename="bengio2003nn.jpeg"))
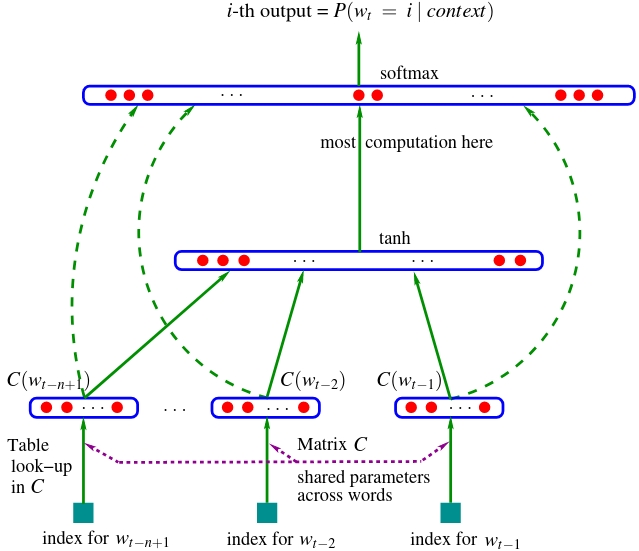
and we have been implementing this over the last few lessons. Now, I’m sure everyone is very excited to go into recurrent neural networks (rnns) and all of their variants and how they work and their diagrams look cool:
from IPython.display import Image, display
display(Image(filename="rnns.png"))
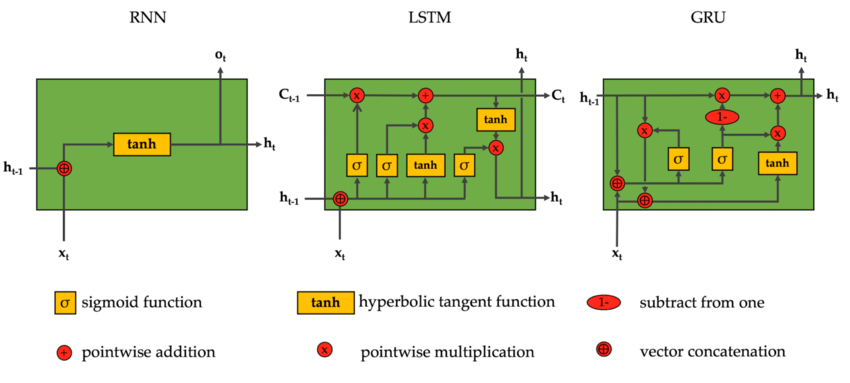
and such models are very exciting and interesting, and we’re going to get a better result. But unfortunately, I think we have to remain here for one more lecture. And the reason for that is we’ve already trained this mlp and we are getting pretty good loss and we have developed a pretty decent understanding of the architecture and how it works. But in train(), we are using loss.backward(), a line of code that we should take an issue with if we want to have a holistic and intuitive understanding of how gradients are actually being calculated and what exactly is going on here. That is, we have been using PyTorch’s autograd and using it to calculate all of our gradients along the way. Here, what we will do is remove the use of loss.backward(), and we will write our backward pass manually, at the level of tensors.
Backprop back in the day#
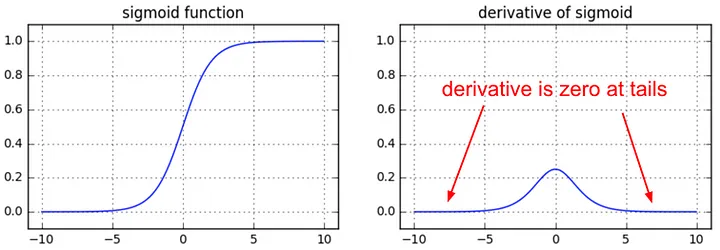
This will prove to be a very useful exercise for the following reasons. Andrej has actually an entire blogpost on this topic: Yes you should understand backprop, where he basically characterizes backprop as a leaky abstraction. And what I mean by that is that backprop doesn’t just make your nns just work magically. It’s not the case that you can just stack up arbitrary lego blocks of differentiable functions and just cross your fingers, do backprop and everything is great. Things don’t just work automatically. It is a leaky abstraction in the sense that you can shoot yourself in the foot if you do not understand its internals. It may magically not work or not work optimally. And you will need to understand how it works under the hood if you’re hoping to debug an issue with it and if you are hoping to address it in your nn. So the blog post goes into some of those examples. So for example, we’ve already covered some of them already. For example, the flat tails of functions such as the \(sigmoid\) or \(tanh\) and how you do not want to saturate them too much because your gradients will die:
from IPython.display import Image, display
display(Image(filename="sigmoid_derivative.jpeg"))
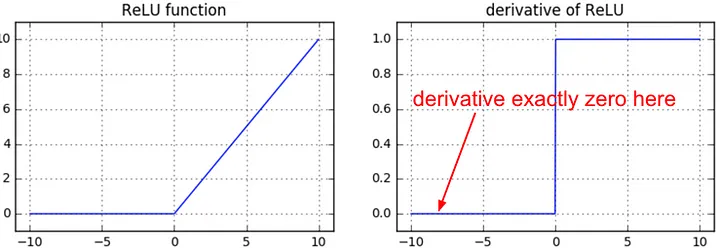
There’s the case of dead neurons, which we’ve already covered as well:
from IPython.display import Image, display
display(Image(filename="relu_derivative.jpeg"))
Also, the case of exploding or vanishing gradients in the case of rnns, which we are about to cover:
from IPython.display import Image, display
display(Image(filename="rnngradients.jpeg"))

And then also you will often come across some examples in the wild:
from IPython.display import Image, display
display(Image(filename="dqnbadclipping.jpeg"))

This is a snippet that Andrej found in a random code base on the internet where they actually have like a very subtle but pretty-major bug in their implementation. And the bug points at the fact that the author of this code does not actually understand backprop. So what they’re trying to do here is they’re trying to clip the loss at a certain maximum value. But actually what they’re trying to do is they’re trying to clip the gradients to have a maximum value instead of trying to clip the loss at a maximum value. And indirectly, they’re basically causing some of the outliers to be actually ignored. Because, when you clip the loss of an outlier, you are setting its gradient to \(0\). And so have a look through this and read through it. But there’s basically a bunch of subtle issues that you’re going to avoid if you actually know what you’re doing. And that’s why I don’t think it’s the case that because PyTorch or other frameworks offer autograd, it is okay for us to ignore how it works. Now, we’ve actually already covered autograd and we wrote micrograd. But micrograd was an autograd engine only at the level of individual scalars. So the atoms were single individual numbers which I don’t think is enough. And I’d like us to basically think about backprop at the level of tensors as well. And so in a summary, I think it’s a good exercise. I think it is very, very valuable. You’re going to become better at debugging nns and making sure that you understand what you’re doing. It is going to make everything fully explicit. So you’re not going to be nervous about what is hidden away from you. Basically, we’re going to emerge stronger! So let’s get into it. A bit of a fun historical note here is that today, manually writing your backward pass by hand is not recommended and no one does it, except for the purposes of exercise and education. But about around \(10\)+ years ago in deep learning, this was fairly standard and in fact pervasive.
from IPython.display import Image, display
display(Image(filename="backwardmemelol.png"))
So at the time, everyone (including Andrej himself) used to write their backward pass manually, by hand. Now, it’s our turn too! Now of course everyone just calls loss.backward(). But, we’ve lost something. I want to give you a few examples of this. So, here’s a \(2006\) paper from Geoffrey Hinton and Ruslan Salakhutdinov in Science that was influential at the time: Reducing the Dimensionality of Data with Neural Networks. And this was training some architectures called restricted Boltzmann machines (rbms). And basically, it’s an autoencoder trained here:
from IPython.display import Image, display
display(Image(filename="rbms.jpeg"))
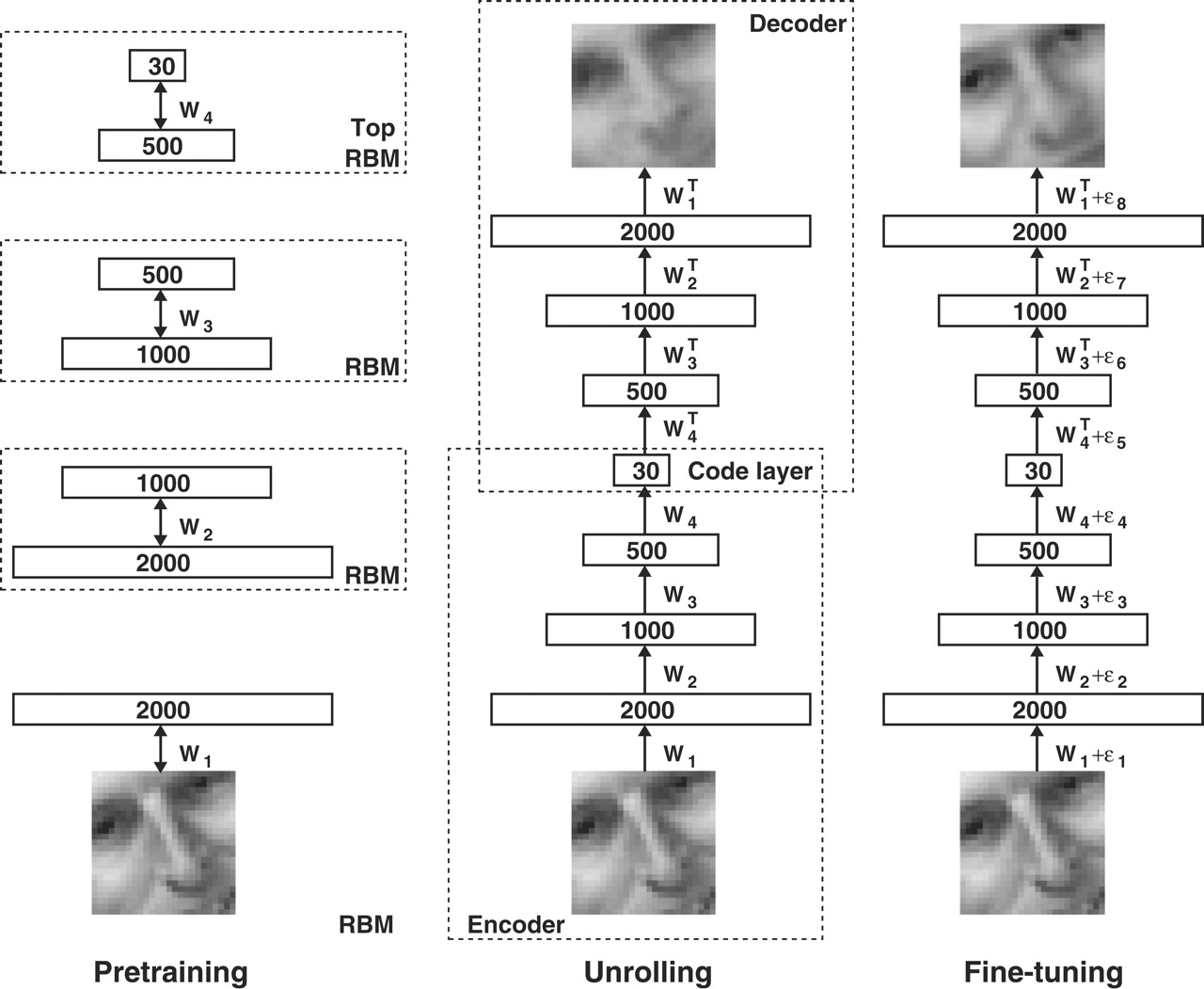
And this is from roughly \(2010\), when Andrej had written a MATLAB library for training (rbms) called matrbm. And this was at the time when Python was not used for deep learning as pervasively as it is now. It was all MATLAB, which was this scientific computing package that everyone would use:
from IPython.display import Image, display
display(Image(filename="matlab.png"))
So we would write MATLAB, which is barely a programming language as well. But it had a very convenient tensor class. And it was this computing environment and you would run here. It would all run on the CPU, of course. But you would have very nice plots to go with it and a built-in debugger. And it was pretty decent. Now, the code in the \(2010\) matrbm package that written for fitting rbms to a large extent is recognizable. Let’s open up the rbmFit.m source code file and see if we can get a rough idea of what is going on. Well first Andrej creates the data and the x, y batches:
...
%Create targets: 1-of-k encodings for each discrete label
u= unique(y);
targets= zeros(N, nclasses);
for i=1:length(u)
targets(y==u(i),i)=1;
end
%Create batches
numbatches= ceil(N/batchsize);
groups= repmat(1:numbatches, 1, batchsize);
groups= groups(1:N);
groups = groups(randperm(N));
for i=1:numbatches
batchdata{i}= X(groups==i,:);
batchtargets{i}= targets(groups==i,:);
end
...
He’s initializing the nn so that it’s got weights as and biases just like we’re used to:
...
%fit RBM
numcases=N;
numdims=d;
numclasses= length(u);
W = 0.1*randn(numdims,numhid);
c = zeros(1,numdims);
b = zeros(1,numhid);
Wc = 0.1*randn(numclasses,numhid);
cc = zeros(1,numclasses);
ph = zeros(numcases,numhid);
nh = zeros(numcases,numhid);
phstates = zeros(numcases,numhid);
nhstates = zeros(numcases,numhid);
negdata = zeros(numcases,numdims);
negdatastates = zeros(numcases,numdims);
Winc = zeros(numdims,numhid);
binc = zeros(1,numhid);
cinc = zeros(1,numdims);
Wcinc = zeros(numclasses,numhid);
ccinc = zeros(1,numclasses);
Wavg = W;
bavg = b;
cavg = c;
Wcavg = Wc;
ccavg = cc;
t = 1;
errors=zeros(1,maxepoch);
...
And then this is the training loop where we actually do the forward pass:
...
for epoch = 1:maxepoch
errsum=0;
if (anneal)
penalty= oldpenalty - 0.9*epoch/maxepoch*oldpenalty;
end
for batch = 1:numbatches
[numcases numdims]=size(batchdata{batch});
data = batchdata{batch};
classes = batchtargets{batch};
%go up
ph = logistic(data*W + classes*Wc + repmat(b,numcases,1));
phstates = ph > rand(numcases,numhid);
if (isequal(method,'SML'))
if (epoch == 1 && batch == 1)
nhstates = phstates;
end
elseif (isequal(method,'CD'))
nhstates = phstates;
end
...
And then here, at this time, they didn’t even necessarily use back propagation to train nns. So this, in particular, implements a lot of the training that we’re doing. It implements contrastive divergence, which estimates a gradient:
...
%go down
negdata = logistic(nhstates*W' + repmat(c,numcases,1));
negdatastates = negdata > rand(numcases,numdims);
negclasses = softmaxPmtk(nhstates*Wc' + repmat(cc,numcases,1));
negclassesstates = softmax_sample(negclasses);
%go up one more time
nh = logistic(negdatastates*W + negclassesstates*Wc + ...
repmat(b,numcases,1));
nhstates = nh > rand(numcases,numhid);
...
And then here, we take that gradient and use it for a parameter update along the lines that we’re used to:
...
%update weights and biases
dW = (data'*ph - negdatastates'*nh);
dc = sum(data) - sum(negdatastates);
db = sum(ph) - sum(nh);
dWc = (classes'*ph - negclassesstates'*nh);
dcc = sum(classes) - sum(negclassesstates);
Winc = momentum*Winc + eta*(dW/numcases - penalty*W);
binc = momentum*binc + eta*(db/numcases);
cinc = momentum*cinc + eta*(dc/numcases);
Wcinc = momentum*Wcinc + eta*(dWc/numcases - penalty*Wc);
ccinc = momentum*ccinc + eta*(dcc/numcases);
W = W + Winc;
b = b + binc;
c = c + cinc;
Wc = Wc + Wcinc;
cc = cc + ccinc;
if (epoch > avgstart)
%apply averaging
Wavg = Wavg - (1/t)*(Wavg - W);
cavg = cavg - (1/t)*(cavg - c);
bavg = bavg - (1/t)*(bavg - b);
Wcavg = Wcavg - (1/t)*(Wcavg - Wc);
ccavg = ccavg - (1/t)*(ccavg - cc);
t = t+1;
else
Wavg = W;
bavg = b;
cavg = c;
Wcavg = Wc;
ccavg = cc;
end
%accumulate reconstruction error
err= sum(sum( (data-negdata).^2 ));
errsum = err + errsum;
end
...
But you can see that basically people are meddling with these gradients directly and inline all by themselves. It wasn’t that common to use an autograd engine. Here’s one more example from Andrej’s paper from \(2014\) called Deep Fragment Embeddings for Bidirectional Image Sentence Mapping. Here, what he was doing is he was aligning images and text:
from IPython.display import Image, display
display(Image(filename="karpathy2014fig2.jpeg"))
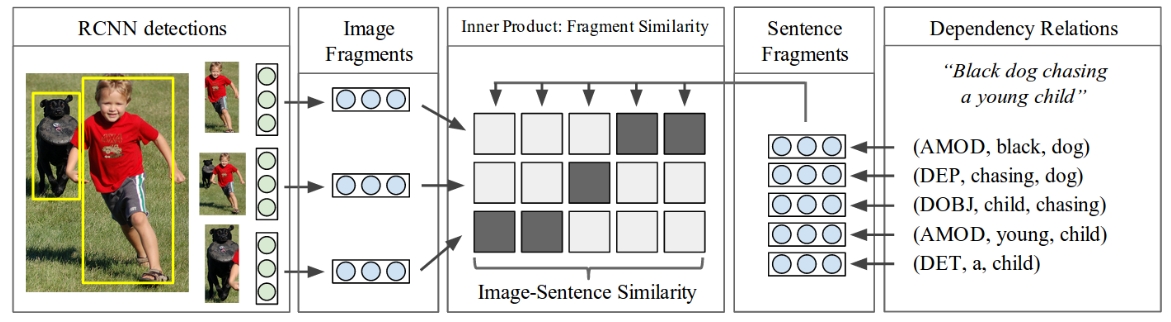
And so it’s kind of like a clip if you’re familiar with it, but instead of working at the level of entire images and entire sentences, he was working on the level of individual objects and little pieces of sentences and he was embedding them calculating a clip-like loss: the cost. Back in 2014, it was standard to implement not just the cost, but also the backward pass manually. Take a look at the DeFragCost function from the paper’s source code:
function [cost_struct, grad, df_CNN] = DeFragCost(theta,decodeInfo,params, oWe,imgFeats,depTrees, rcnn_model)
% returns cost, gradient, and gradient wrt image vectors which
% can be forwarded to the CNN for finetuning outside of this
domil = getparam(params, 'domil', false);
useglobal = getparam(params, 'useglobal', true);
uselocal = getparam(params, 'uselocal', true);
gmargin = params.gmargin;
lmargin = params.lmargin;
gscale = params.gscale;
lscale = params.lscale;
thrglobalscore = params.thrglobalscore;
smoothnum = params.smoothnum;
maxaccum = params.maxaccum;
finetuneCNN = false;
df_CNN = 0;
% unpack parameters
[Wi2s, Wsem] = stack2param(theta, decodeInfo);
cost = 0;
N = length(depTrees); % number of samples
% forward prop all image fragments and arrange them into a single large matrix
imgVecsCell = cell(1, N);
imgVecICell = cell(1, N);
if finetuneCNN
% forward RCNN
imgVecs = andrej_forwardRCNN(imgFeats, rcnn_model, params);
for i=1:N
imgVecICell{i} = ones(size(imgFeats{i}.codes,1), 1)*i;
end
else
for i=1:N
imgVecsCell{i} = imgFeats{i}.codes;
end
imgVecs = cat(1, imgVecsCell{:});
for i=1:N
imgVecICell{i} = ones(size(imgVecsCell{i},1), 1)*i;
end
end
imgVecI = cat(1, imgVecICell{:});
allImgVecs = Wi2s * imgVecs'; % the mapped vectors are now columns
Ni = size(allImgVecs,2);
% forward prop all sentences and arrange them
sentVecsCell = cell(1, N);
sentTriplesCell = cell(1, N);
sentVecICell = cell(1, N);
for i = 1:N
[z, ts] = ForwardSent(depTrees{i},params,oWe,Wsem);
sentVecsCell{i} = z;
sentTriplesCell{i} = ts;
sentVecICell{i} = ones(size(z,2), 1)*i;
end
sentVecI = cat(1, sentVecICell{:});
allSentVecs = cat(2, sentVecsCell{:});
Ns = size(allSentVecs, 2);
% compute fragment scores
dots = allImgVecs' * allSentVecs;
% compute local objective
if uselocal
MEQ = bsxfun(@eq, imgVecI, sentVecI'); % indicator array for what should be high and low
Y = -ones(size(MEQ));
Y(MEQ) = 1;
if domil
% miSVM formulation: we are minimizing over Y in the objective,
% what follows is a heuristic for it mentioned in miSVM paper.
fpos = dots .* MEQ - 9999 * (~MEQ); % simplifies things
Ypos = sign(fpos);
ixbad = find(~any(Ypos==1,1));
if ~isempty(ixbad)
[~, fmaxi] = max(fpos(:,ixbad), [], 1);
Ypos = Ypos + sparse(fmaxi, ixbad, 2, Ni, Ns); % flip from -1 to 1: add 2
end
Y(MEQ) = Ypos(MEQ); % augment Y in positive bags
end
% weighted fragment alignment objective
marg = max(0, lmargin - Y .* dots); % compute margins
W = zeros(Ni, Ns);
for i=1:Ns
ypos = Y(:,i)==1;
yneg = Y(:,i)==-1;
W(ypos, i) = 1/sum(ypos);
W(yneg, i) = 1/(sum(yneg));
end
wmarg = W .* marg;
lcost = lscale * sum(wmarg(:));
cost = cost + lcost;
end
% compute global objective
if useglobal
% forward scores in all regions
SG = zeros(N,N);
SGN = zeros(N,N); % the number of values (for mean)
accumsis = cell(N,N);
for i=1:N
for j=1:N
d = dots(imgVecI == i, sentVecI == j);
if thrglobalscore, d(d<0) = 0; end
if maxaccum
[sv, si] = max(d, [], 1); % score will be max (i.e. we're finding support of each fragment in image)
accumsis{i,j} = si; % remember switches for backprop
s = sum(sv);
else
s = sum(d(:)); % score is sum
end
nnorm = size(d,2); % number of sent fragments
nnorm = nnorm + smoothnum;
s = s/nnorm;
SG(i,j) = s;
SGN(i,j) = nnorm;
end
end
% compute the cost
gcost = 0;
cdiffs = zeros(N,N);
rdiffs = zeros(N,N);
for i=1:N
% i is the pivot. It should have higher score than col and row
% col term
cdiff = max(0, SG(:,i) - SG(i,i) + gmargin);
cdiff(i) = 0; % nvm score with self
cdiffs(:, i) = cdiff; % useful in backprop
% row term
rdiff = max(0, SG(i,:) - SG(i,i) + gmargin);
rdiff(i) = 0;
rdiffs(i, :) = rdiff; % useful in backprop
gcost = gcost + sum(cdiff) + sum(rdiff);
end
gcost = gscale * gcost;
cost = cost + gcost;
end
ltop = zeros(Ni, Ns);
if uselocal
% backprop local objective
ltop = ltop - lscale * (marg > 0) .* Y .* W;
end
if useglobal
% backprop global objective
% backprop margin
dsg = zeros(N,N);
for i=1:N
cd = cdiffs(:,i);
rd = rdiffs(i,:);
% col term backprop
dsg(i,i) = dsg(i,i) - sum(cd > 0);
dsg(:,i) = dsg(:,i) + (cd > 0);
% row term backprop
dsg(i,i) = dsg(i,i) - sum(rd > 0);
dsg(i,:) = dsg(i,:) + (rd > 0);
end
% backprop into scores
ltopg = zeros(size(ltop));
for i=1:N
for j=1:N
% backprop through the accumulation function
if maxaccum
% route the gradient along in each column. bit messy...
gradroute = dsg(i,j) / SGN(i,j);
mji = find(sentVecI == j);
mii = find(imgVecI == i);
accumsi = accumsis{i,j};
for q=1:length(mji)
miy = mii(accumsi(q));
mix = mji(q);
if thrglobalscore
if dots(miy,mix) > 0
ltopg(miy, mix) = gradroute;
end
else
ltopg(miy, mix) = gradroute;
end
end
else
d = dots(imgVecI == i, sentVecI == j);
dd = ones(size(d)) * dsg(i,j) / SGN(i,j);
if thrglobalscore
dd(d<0) = 0;
end
ltopg(imgVecI == i, sentVecI == j) = dd;
end
end
end
ltop = ltop + gscale * ltopg;
end
% backprop into fragment vectors
allDeltasImg = allSentVecs * ltop';
allDeltasSent = allImgVecs * ltop;
% backprop image mapping
df_Wi2s = allDeltasImg * imgVecs;
if finetuneCNN
% derivative wrt CNN data so that we can pass on gradient to RCNN
df_CNN = allDeltasImg' * Wi2s;
end
% backprop sentence mapping
df_Wsem = BackwardSents(depTrees,params,oWe,Wsem,sentVecsCell,allDeltasSent);
cost_struct = struct();
cost_struct.raw_cost = cost;
cost_struct.reg_cost = params.regC/2 * sum(theta.^2);
cost_struct.cost = cost_struct.raw_cost + cost_struct.reg_cost;
%[grad,~] = param2stack(df_Wi2s, df_Wsem);
grad = [df_Wi2s(:); df_Wsem(:);]; % for speed hardcode param2stack
grad = grad + params.regC * theta; % regularization term gradient
end
Around \(2014\) it was standard to implement not just the cost but also the backward pass manually. So there he calculates the image embeddings sentence embeddings, sentence embeddings, the scores and the loss function. And after the loss function is calculated, he backwards through the nn and he appends a regularization term. So everything was done by hand manually, and you would just write out the backward pass. And then you would use a gradient checker to make sure that your numerical estimate of the gradient agrees with the one you calculated during backprop. This was very standard for a long time. Today, of course, it is standard to use an autograd engine. But it was definitely useful, and I think people sort of understood how these nns work on a very intuitive level. Therefore, it’s still a good exercise.
Manually implementing a backward pass#
Okay, so just as a reminder that we’re going to keep everything the same from our previous lecture. So we’re still going to have a two-layer multi-layer perceptron with a batchnorm layer. So the forward pass will be basically identical to this lecture. But here, we’re going to get rid of loss.backward(). And instead, we’re going to write the backward pass manually. Apart from that, we’re going to keep everything the same. So the forward pass will be basically identical to the previous lesson, etc. We are simply just going to write the backward pass manually. Here’s the starter code for this lecture:
import random
random.seed(42)
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt # for making figures
if IN_COLAB:
%matplotlib inline
else:
%matplotlib ipympl
SEED = 2147483647
# read in all the words
words = open("names.txt", "r").read().splitlines()
print(len(words))
print(max(len(w) for w in words))
print(words[:8])
32033
15
['emma', 'olivia', 'ava', 'isabella', 'sophia', 'charlotte', 'mia', 'amelia']
# build the vocabulary of characters and mappings to/from integers
chars = sorted(list(set("".join(words))))
ctoi = {s: i + 1 for i, s in enumerate(chars)}
ctoi["."] = 0
itoc = {i: s for s, i in ctoi.items()}
vocab_size = len(itoc)
print(itoc)
print(vocab_size)
{1: 'a', 2: 'b', 3: 'c', 4: 'd', 5: 'e', 6: 'f', 7: 'g', 8: 'h', 9: 'i', 10: 'j', 11: 'k', 12: 'l', 13: 'm', 14: 'n', 15: 'o', 16: 'p', 17: 'q', 18: 'r', 19: 's', 20: 't', 21: 'u', 22: 'v', 23: 'w', 24: 'x', 25: 'y', 26: 'z', 0: '.'}
27
block_size = 3
def build_dataset(words):
x, y = [], []
for w in words:
context = [0] * block_size
for ch in w + ".":
ix = ctoi[ch]
x.append(context)
y.append(ix)
context = context[1:] + [ix] # crop and append
x = torch.tensor(x)
y = torch.tensor(y)
print(x.shape, y.shape)
return x, y
random.shuffle(words)
n1 = int(0.8 * len(words))
n2 = int(0.9 * len(words))
xtrain, ytrain = build_dataset(words[:n1]) # 80%
xval, yval = build_dataset(words[n1:n2]) # 10%
xtest, ytest = build_dataset(words[n2:]) # 10%
torch.Size([182625, 3]) torch.Size([182625])
torch.Size([22655, 3]) torch.Size([22655])
torch.Size([22866, 3]) torch.Size([22866])
Now, here, we’ll introduce a utility function that we’re going to use later to compare the gradients. So in particular, we are going to have the gradients that we estimate manually ourselves. And we’re going to have gradients that PyTorch calculates. And we’re going to be checking for correctness, assuming, of course, that PyTorch is correct.
# utility function we will use later when comparing manual gradients to PyTorch gradients
def cmp(s, dt, t):
ex = torch.all(dt == t.grad).item()
app = torch.allclose(dt, t.grad)
maxdiff = (dt - t.grad).abs().max().item()
print(
f"{s:15s} | exact: {str(ex):5s} | approximate: {str(app):5s} | maxdiff: {maxdiff}"
)
Then, here, we have an initialization function that we are quite used to, where we create all the parameters:
def define_nn(
n_hidden=64,
n_embd=10,
w1_factor=5 / 3,
b1_factor=0.1,
w2_factor=0.1,
b2_factor=0.1,
bngain_factor=0.1,
bnbias_factor=0.1,
):
global g, C, w1, b1, w2, b2, bngain, bnbias
g = torch.Generator().manual_seed(SEED)
C = torch.randn((vocab_size, n_embd), generator=g)
input_size = n_embd * block_size
output_size = vocab_size
# Layer 1
w1 = (
torch.randn((input_size, n_hidden), generator=g)
* w1_factor
/ ((input_size) ** 0.5)
)
b1 = (
torch.randn(n_hidden, generator=g) * b1_factor
) # using b1 just for fun, it's useless because of batchnorm layer
# Layer 2
w2 = torch.randn(n_hidden, vocab_size, generator=g) * w2_factor
b2 = torch.randn(vocab_size, generator=g) * b2_factor
# BatchNorm parameters
bngain = torch.ones((1, n_hidden)) * bngain_factor + 1.0
bnbias = torch.zeros((1, n_hidden)) * bnbias_factor
# Note: We are initializating many of these parameters in non-standard ways
# because sometimes initializating with e.g. all zeros could mask an incorrect
# implementation of the backward pass.
parameters = [C, w1, b1, w2, b2, bngain, bnbias]
print(sum(p.nelement() for p in parameters))
for p in parameters:
p.requires_grad = True
return parameters
Now, you will note that we changed the initialization a little bit to be small numbers. So normally you would set the biases to be all \(0\). Here, I’m setting them to be small random numbers. And I’m doing this because if your variables are all \(0\), or initialized to exactly \(0\), sometimes what can happen is that can mask an incorrect implementation of a gradient. Because when everything is \(0\), it sort of like simplifies and gives you a much simpler expression of the gradient than you would otherwise get. And so by making it small numbers, we are trying to unmask those potential errors in these calculations. You might also notice that we are using b1 in the first layer. We are using a bias despite batchnorm right afterwards. So this would typically not be what you’d do as we talked about the fact that you don’t need a bias. But we are doing this here just for fun, because we are going to have a gradient w.r.t. it and we can check that we are still calculating it correctly even though this bias is spurious.
batch_size = 32
def construct_minibatch():
ix = torch.randint(0, xtrain.shape[0], (batch_size,), generator=g)
xb, yb = xtrain[ix], ytrain[ix]
return xb, yb
So this function calculates a single batch. Then we will define a forward pass function:
def forward(xb, yb):
emb = C[xb] # embed the characters into vectors
embcat = emb.view(emb.shape[0], -1) # concatenate the vectors
# Linear layer 1
hprebn = embcat @ w1 + b1 # hidden layer pre-activation
# BatchNorm layer
bnmeani = 1 / batch_size * hprebn.sum(0, keepdim=True)
bndiff = hprebn - bnmeani
bndiff2 = bndiff**2
bnvar = (
1 / (batch_size - 1) * (bndiff2).sum(0, keepdim=True)
) # note: Bessel's correction (dividing by n-1, not n)
bnvar_inv = (bnvar + 1e-5) ** -0.5
bnraw = bndiff * bnvar_inv
hpreact = bngain * bnraw + bnbias
# Non-linearity
h = torch.tanh(hpreact)
# Linear layer 2
logits = h @ w2 + b2 # output layer
# cross entropy loss (same as F.cross_entropy(logits, Yb))
logit_maxes = logits.max(1, keepdim=True).values
norm_logits = logits - logit_maxes # subtract max for numerical stability
counts = norm_logits.exp()
counts_sum = counts.sum(1, keepdims=True)
counts_sum_inv = counts_sum**-1
probs = counts * counts_sum_inv
logprobs = probs.log()
globals().update(locals()) # make variables defined so far globally-accessible
loss = -logprobs[range(batch_size), yb].mean()
intermediate_values = [
logprobs,
probs,
counts,
counts_sum,
counts_sum_inv,
norm_logits,
logit_maxes,
logits,
h,
hpreact,
bnraw,
bnvar_inv,
bnvar,
bndiff2,
bndiff,
hprebn,
bnmeani,
embcat,
emb,
]
return intermediate_values, loss
def backward(parameters, fp_intermed_values, loss):
# PyTorch backward pass
for p in parameters:
p.grad = None
for t in fp_intermed_values:
t.retain_grad()
loss.backward()
This forward() is now significantly expanded compared to what we are used to. The reason our forward pass is longer is for two reasons. Number one, before we just had an f.cross_entropy(), but here we are bringing back an explicit implementation of the loss function. And number two, we have broken up the implementation into manageable chunks, so we have a lot more intermediate tensors along the way in the forward pass. And that’s because we are about to go backwards and calculate the gradients in this backprop, from the bottom (loss) to the top (…, emb, C, xb). So we’re going to go upwards and just like we have for example the logprobs in this forward pass, in the backward pass we are going to have a dlogprobs which is going to store the derivative of the loss w.r.t. the logprobs tensor (\(\dfrac{\partial **loss**}{\partial logprobs}\)). And so in our manual implementation of backprop, we are going to be prepending d to every one of these tensors and calculating it along the way of this backprop. As an example, we have a bnraw here, so we’re going to be calculating a dbnraw (\(\dfrac{\partial **loss**}{\partial bnraw}\)). Also, in the backward() function, before the loss.backward() call, we are calling t.retain_grad() and thus telling PyTorch that we want to retain the graph of all of these intermediate values. This is because:
in exercise 1 (coming up) we are going to calculate the backward pass, so we’re going to calculate all these
dvariables and use thecmpfunction we’ve introduced above to check our correctness w.r.t. what PyTorch is telling us. This is going to be exercise 1, where we will backprop through this entire graph (starting from thelossand going upward through the intermediate values). Then,in exercise 2 we will fully break up the loss and backprop through it manually in all the little atomic pieces that make it up. But then we’re going to collapse the loss into a single cross entropy call and instead we’re going to analytically derive using math and paper and pencil the gradient of the loss w.r.t. the logits and instead of backproping through all of its little chunks, one at a time, we’re just going to analytically derive what that gradient is and we’re going to implement that, which is much more efficient as we’ll see in a bit. Next,
for exercise 3 we’re going to do the exact same thing for batchnorm. We’re going to use pen and paper and calculus to derive the gradient through the batchnorm layer. So we’re going to calculate the backward pass through the batchnorm layer in a much more efficient expression, instead of backprop through all of its little pieces independently. And then,
in exercise 4 we’re going to put it all together and this is the full code of training this two layer mlp and we’re going to basically insert our manual backprop and we’re going to take out
loss.backward()and you will basically see that we can get all the same results using fully our own code and the only thing we’re going to be using from PyTorch istorch.tensorto make the calculations efficient. But otherwise, you will understand fully what it means to forward and backward through the nn and train it and I think that’ll be awesome so let’s get to it.
Okay, let’s now define our nn and do one forward and one backward pass on it:
parameters = define_nn()
xb, yb = construct_minibatch()
fp_intermed_values, loss = forward(xb, yb)
backward(parameters, fp_intermed_values, loss)
4137
Exercise 1: implementing the backward pass#
Now, exercise 1: implementing the backward pass:
We’ll start with dlogprobs, which basically means we are going to start with calculating the gradient of the loss w.r.t. all the elements of logprobs tensor: \(\dfrac{\partial \textbf{loss}}{\partial \textbf{logprobs}}\). So, dlogprobs will have the same shape as logprobs:
logprobs.shape
torch.Size([32, 27])
Now, how does logprobs influence the loss? Like this: -logprobs[range(batch_size), yb].mean(). Just as a reminder, yb is only just an array of the correct indeces:
yb
tensor([ 8, 14, 15, 22, 0, 19, 9, 14, 5, 1, 20, 3, 8, 14, 12, 0, 11, 0,
26, 9, 25, 0, 1, 1, 7, 18, 9, 3, 5, 9, 0, 18])
And so by doing logprobs[range(batch_size), yb], what we are essentially doing is for each row i of the logprobs tensor (of size batch_size), we are plucking out the element at column index yb[i]. For example, from row 0 we would be getting the element from column yb[0] == 1, from row 1 we would be getting the element from column yb[1] == 12, and so on. Therefore, the elements inside the logprobs[range(batch_size), yb] could be alternatively calculated as such:
logprobslist = [logprobs[i, yb[i]] for i in range(batch_size)]
Here is the proof by assertion that logprobslist is the same as logprobs:
logprobslist = [logprobs[i, yb[i]].item() for i in range(batch_size)]
assert logprobs[range(batch_size), yb].tolist() == logprobslist
So these elements get plucked out from logprobs and then the negative of their mean becomes the loss. It is always nice to work with simpler examples in order to understand the numerical form of derivatives. What’s going on here is once we’ve plucked out these examples, we’re taking the mean and then the negative (-logprobs[range(batch_size), yb].mean()). So the loss basically, to write it in a simpler way, is the negative of the mean of e.g. \(3\) values:
loss = -(a + b + c) / 3
loss = -a/3 - b/3 - c/3
That would be how we achieve the mean of three numbers a, b, c (although we actually have \(32\) numbers here). But therefore the derivative of this toy loss w.r.t. a would basically be just:
dloss/da = -1/3
So you can see that if we don’t just have \(3\) numbers (a, b, c), but we have \(32\) numbers, then dloss by dk (where k is every one of those \(32\) numbers) is going to be: \(1/32\) or just \(\frac{1}{batch\_size}\) more generally. Now, what about the other elements inside logprobs? Remember, logprobs is a large array with a logprobs.shape of \(32 \times 27\) (\(864\) numbers in total) and only:
logprobs[range(batch_size), yb].shape
torch.Size([32])
\(32\) of these numbers participate in the loss calculation. So, what about the derivative of all the other \(832\) numbers of the logprobs tensor, meaning the rest of the elements that do not get plucked out? Well, their gradient intuitively is \(0\). Simply because they do not participate in the loss calculation. They are left out. So, since most of these numbers inside the logprobs tensor does not feed into the loss, if we were to change these numbers, then the value of loss wouldn’t change. Which is the equivalent way of saying that the derivative of the loss w.r.t. them is zero. They don’t impact it. So here’s a way to implement this derivative then: we create a tensor of zeros exactly in the shape of logprobs and then fill in the derivative value -1/batch_size inside exactly these indeces: [range(batch_size), yb]. Therefore:
dlogprobs = torch.zeros_like(logprobs)
dlogprobs[range(batch_size), yb] = -1.0 / batch_size
Then this is the candidate derivative for dlogprobs. Let’s call our assertion function to compare with the actual derivative computed by PyTorch and check whether our manually calculated derivative is correct:
cmp("logprobs", dlogprobs, logprobs)
logprobs | exact: True | approximate: True | maxdiff: 0.0
Cool! So let’s look at the definition of the cmp function:
def cmp(s, dt, t):
ex = torch.all(dt == t.grad).item()
app = torch.allclose(dt, t.grad)
maxdiff = (dt - t.grad).abs().max().item()
print(f'{s:15s} | exact: {str(ex):5s} | approximate: {str(app):5s} | maxdiff: {maxdiff}')
What it does is that it basically receives the calculated value provided by us, which is dt and then checks whether it is exactly equal to t.grad as calculated by PyTorch. This makes sure that all of the elements are exactly equal. After that, it calculates for approximate equality because of floating point issues using torch.allclose which has a little bit of a wiggle available because sometimes you can get very, very close. But if you use a slightly different calculation, because of floating point, you can’t get very, very close. Generally, because of floating point arithmetic, you can get a slightly different result. So this second call checks for an approximately equal result. And then it finds the maximum, basically the value that has the highest difference, and what is the difference, and the absolute value difference between those two. At the end it prints whether we have an exact equality, an approximate equality, and what is the largest difference. In our case, we have an exact equality. And so therefore, of course, we also have an approximate equality, and the maximum difference is exactly zero. So basically, our dlogprobs is exactly equal to what PyTorch calculated to be logprobs.grad in its backpropagation. So far, we’re doing pretty well. Okay, so let’s now continue our manual backprop. We know that logprobs depends on probs through a .log() call. So a log is applied to all the elements of probs, element-wise. Now, if we want dprobs: \(\dfrac{\partial loss}{\partial probs} = \dfrac{\partial loss}{\partial logprobs}\cdot\dfrac{\partial logprobs}{\partial probs}\), then, well let’s ask WolframAlpha what the derivative of log(x) is w.r.t. x: \(\dfrac{d(log(x))}{dx} = \dfrac{1}{x}\). Therefore we write out the derivative and because we are doing backprop and thus applying the chain rule, we want to chain it to the previous result:
dprobs = (1.0 / probs) * dlogprobs
cmp("probs", dprobs, probs)
probs | exact: True | approximate: True | maxdiff: 0.0
Now, notice what happens if your probs is very very close to \(1.0\), that means that the nn is predicting the character correctly, then dprobs = (1.0 / 1.0) * dlogprobs = dlogprobs and thus dlogprobs just gets passed through. But if probs are very low, then the fraction part that is multiplied by dlogprobs will be boosted instead of dlogprobs. So what this line is doing intuitively is it is boosting the the gradient of the examples that have a very low probability currently assigned. Next up is counts_sum_inv. So we want dcounts_sum_inv (\(\dfrac{\partial loss}{\partial counts\_sum\_inv}\)). But let’s just pause for a moment and explain what is happening until the calculation of counts_sum_inv, in case all this is a bit confusing:
...
# Linear layer 2
logits = h @ w2 + b2 # output layer
# cross entropy loss (same as F.cross_entropy(logits, Yb))
logit_maxes = logits.max(1, keepdim=True).values
norm_logits = logits - logit_maxes # subtract max for numerical stability
counts = norm_logits.exp()
counts_sum = counts.sum(1, keepdims=True)
counts_sum_inv = counts_sum**-1
probs = counts * counts_sum_inv
...
We have the logits that come out of the nn. Then we are finding the maximum in each row that we then subtract from the logits for purposes of numerical stability. Then, because some of the logits may take on too large values we end up exponentiating (this is done just for safety, numerically). This exponentiation yields our counts. And then, we take the sum of these counts. Using this counts_sum, we normalize the counts so that all of the probs sum to \(1\). But basically, all that’s happening here is we got the logits, we want to exponentiate all of them, and we want to normalize the counts to create our probabilities, it’s just that we have defined this set of intermediate calculations across multiple lines. Ok, so what should be dcounts_sum_inv? Now, we actually have to be careful here because we have to scrutinize and be careful with the shapes. So, counts.shape and counts_sum_inv.shape are different:
print(counts.shape, counts_sum_inv.shape)
assert counts.shape != counts_sum_inv.shape
torch.Size([32, 27]) torch.Size([32, 1])
So during the multiplication probs = counts * counts_sum_inv, there is an implicit broadcasting that PyTorch does. Because what it needs to do is take one column of \(32 \times 1\) that is counts_sum_inv and replicate it horizontally \(27\) times in order to align these two tensors so it can do an element-wise multiplication. Using a toy example, this is what this looks like:
# c = a * b, but with tensors:
# a[3x3] * b[3,1] --->
# a11*b1 a12*b1 a13*b1
# a21*b2 a22*b2 a23*b2
# a31*b3 a32*b3 a33*b3
# c[3x3]
In this example, in order for \(a[3\times3]\) to multiply \(b[3\times1]\), we have to replicate \(3\) times the vertical column \([b1, b2, b3]^T\) horizontally. And then do the actual multiplication. And this is exactly what PyTorch does in this situation. Meaning, in order to do \(c = a \cdot b\) (\(c[3\times3] = a[3\times3] \cdot b[3\times1]\)) it:
first replicates \(b\) across the column dimension (\(1\)): \(b \rightarrow b\_replicated\) (\(b[3\times1] \rightarrow b[3\times3]\))
then it does the multiplication \(c = a \cdot b\_replicated\) (\(c[3\times3] = a[3\times3] \cdot b[3\times3]\))
Therefore, if we wanted to find \(\dfrac{\partial c}{\partial a}\), then that would equal be \(a\_replicated\) (and not \(a\)). What the replication operation means in terms of the computational graph is that \(a\) in this case is being fed to multiple outputs. Thus, as we discussed in micrograd (lesson 1), during the backward pass, the correct thing to do in this case is to sum all the gradients that arrive at any one node (i.e. \(a\)). So if a node is used multiple times, the gradients for all of its uses sum during backprop. This means that since e.g. \(b1\) is used multiple times in each column of \(c\), therefore the right thing to do here would be to sum horizontally across all the columns:
da = a_replicated = a.sum(1, keepdim=True)
Equivalently, probs = counts * counts_sum_inv, is broken up into to operations as well:
first, the replication: \(counts\_sum\_inv \rightarrow counts\_sum\_inv\_replicated\) (\(counts\_sum\_inv[32\times1] \rightarrow counts\_sum\_inv[32\times27]\))
then, the multiplication: \(probs = counts \cdot counts\_sum\_inv\_replicated\) (\(probs[32\times27] = counts[32\times27] \cdot counts\_sum\_inv[32\times27]\))
And therefore dcounts_sum_inv (\(\dfrac{\partial loss}{\partial counts\_sum\_inv} = \dfrac{\partial loss}{\partial probs} \dfrac{\partial probs}{\partial counts\_sum\_inv}\)):
dcounts_sum_inv = (counts * dprobs).sum(
1, keepdim=True
) # multiply by `dprobs` because of chain rule and keepdim=True to keep the column dimension
assert dcounts_sum_inv.shape == counts_sum_inv.shape # shapes are equals
cmp("counts_sum_inv", dcounts_sum_inv, counts_sum_inv)
counts_sum_inv | exact: True | approximate: True | maxdiff: 0.0
Again, this derivative is exactly correct. Let’s also backprop into counts. Similarly, dcounts is:
dcounts = counts_sum_inv * dprobs
assert dcounts.shape == counts.shape
with no additional summation required here since there is a broadcasting going on that will yield a derivative with a shape that is equivalent to the shape of the counts tensor. But we can’t call cmp and check the correctness of dcounts just yet. The reason is that besides being used to calculate probs, it is also being used in another branch to calculate counts_sum_inv. So, even though we have calculated the first contribution of it: \(\dfrac{\partial loss}{\partial probs}\cdot\dfrac{\partial probs}{\partial counts}\), we still have to calculate the second contribution of it: \(\dfrac{\partial loss}{\partial counts\_sum}\cdot\dfrac{\partial counts\_sum}{\partial counts}\). To continue with this branch, we now want to calculate dcounts_sum: \(\dfrac{\partial loss}{\partial counts\_sum} = \dfrac{\partial counts\_sum\_inv}{\partial counts\_sum}\cdot\dfrac{\partial loss}{\partial counts\_sum\_inv}\). With the help of WolframAlpha:
dcounts_sum = (-(counts_sum**-2)) * dcounts_sum_inv
cmp("counts_sum", dcounts_sum, counts_sum)
counts_sum | exact: True | approximate: True | maxdiff: 0.0
Cool. Next, moving along, we want to backprop through the preceding operation: counts_sum = counts.sum(1, keepdims=True). This means we want to now calculate the additional dcounts component: \(\dfrac{\partial loss}{\partial counts} = \dfrac{\partial loss}{\partial counts\_sum}\cdot\dfrac{\partial counts \_sum}{\partial counts}\). If we remember from micrograd, the sum operation basically acts just like a router, allowing the gradient (dcounts_sum, in our case) to distribute equally to all the input during the backward flow. In other words, to use a toy example:
# b = sum(a), but with tensors:
# b[3,1] = a[3x3].sum(1) --->
# a11 a12 a13 ---> b1 (= a11 + a12 + a13)
# a21 a22 a23 ---> b2 (= a21 + a22 + a23)
# a31 a32 a33 ---> b3 (= a31 + a32 + a33)
Therefore considering that \(a\) and \(b\) are multi-dimensional tensors: \(\dfrac{\partial b_{3\times1}}{\partial a_{3\times3}} = \dfrac{\partial{\sum a_{3\times3}}}{\partial a_{3\times3}} = \dfrac{\partial \textbf{1}_{3\times3}^T a_{3\times3}}{\partial a_{3\times3}} = \textbf{1}_{3\times3}\). Therefore, similarly, \(\dfrac{\partial counts\_sum}{\partial counts} = \textbf{1}\), where the matrix \(\textbf{1}\) has the shape of counts. Therefore, we can now add the calculated second component \(\dfrac{\partial counts\_sum}{\partial counts}\dfrac{\partial loss}{\partial counts\_sum}\) to dcounts. And since there is no extra component that makes up dcounts we can do:
dcounts += torch.ones_like(counts) * dcounts_sum
And now dcounts is equal to: \(\dfrac{\partial loss}{\partial counts} = \dfrac{\partial loss}{\partial probs}\cdot\dfrac{\partial probs}{\partial counts} + \dfrac{\partial loss}{\partial counts\_sum}\cdot\dfrac{\partial counts\_sum}{\partial counts}\). And now, we can check for correctness:
cmp("counts", dcounts, counts)
counts | exact: True | approximate: True | maxdiff: 0.0
Awesome! The match is exact, which of course means that once again we have correctly calculated the gradient of yet-another node, and our smooth manual backproping journey continues! So hopefully we should be getting a hang of this now. Now, dnorm_logits is easy:
dnorm_logits = counts * dcounts
cmp("norm_logits", dnorm_logits, norm_logits)
norm_logits | exact: True | approximate: True | maxdiff: 0.0
since \(\dfrac{\partial loss}{\partial norm\_logits} = \dfrac{\partial counts}{\partial norm\_logits}\cdot\dfrac{\partial loss}{\partial counts} = \dfrac{\partial e^{norm\_logits}}{\partial norm\_logits}\cdot\dfrac{\partial loss}{\partial counts} = e^{norm\_logits}\cdot\dfrac{\partial loss}{\partial counts} = counts\cdot\dfrac{\partial loss}{\partial counts}\). Let’s continue. Next up is norm_logits = logits - logit_maxes. So now we care about finding dlogits and dlogit_maxes. We have to be careful here again as the shapes are not the same:
norm_logits.shape, logits.shape, logit_maxes.shape
(torch.Size([32, 27]), torch.Size([32, 27]), torch.Size([32, 1]))
This means that when the subtraction happens there is going to be an implicit broadcasting happening:
# c = a - b, but with tensors: a[3x3], b[3x1], c[3x3]
# c11 c12 c13 = a11 a12 a13 b1
# c21 c22 c23 = a21 a22 a23 - b2
# c31 c32 c33 = a31 a32 a33 b3
# so e.g. c32 = a32 - b3
For calculating dlogits we care about finding the (first) component \(\dfrac{\partial norm\_logits}{\partial logits}\dfrac{\partial loss}{\partial norm\_logits} = \dfrac{\partial loss}{\partial norm\_logits}\). And therefore:
dlogits = dnorm_logits.clone()
Now, like for dcounts previously, we cannot yet check for the correctness of dlogits because there is still a second component that should be added to the first one to make up the complete dlogits gradient \(\dfrac{\partial loss}{\partial logits}\). Before we calculate that let’s first find dlogit_maxes: \(\dfrac{\partial loss}{\partial logit\_maxes} = \dfrac{\partial norm\_logits}{\partial logit\_maxes}\dfrac{\partial loss}{\partial norm\_logits} = -\dfrac{\partial loss}{\partial norm\_logits}\), which essentially means: dlogit_maxes = -dnorm_logits. Now remember, because we are dealing with tensors and logit_maxes has a shape of \(32\times1\), that means that -dnorm_logits, whose shape is \(32\times27\), must be summed along the column axis in order for dlogits_maxes to become a \(32\times1\) tensor (the same shape as logit_maxes). Therefore:
dlogit_maxes = (-dnorm_logits).sum(1, keepdim=True)
cmp("logit_maxes", dlogit_maxes, logit_maxes)
logit_maxes | exact: True | approximate: True | maxdiff: 0.0
Next up is: logit_maxes = logits.max(1, keepdim=True).values. Now, this is the line out of which we will find the second derivative component of dlogits: \(\dfrac{\partial logit\_maxes}{\partial logits}\cdot\dfrac{\partial loss}{\partial logit\_maxes}\). But what is \(\dfrac{\partial logit\_maxes}{\partial logits}\) lossin this case? Before we answer this question, let’s pause here briefly and look at these logit_maxes, and especially their gradients. We’ve talked previously in the previous lesson that the only reason we’re doing this is for the numerical stability of the softmax that we are implementing here. And we talked about how if you take these logits for any one of these examples, so one row of this logits tensor, if you add or subtract any value equally to all the elements, then the value of the probs will be unchanged. You’re not changing the softmax. The only thing that this is doing is it’s making sure that the subsequent exp() operation doesn’t overflow. And the reason we’re using a max is because then we are guaranteed that each row of logits, the highest number, is \(0\). Basically, that has repercussions. If it is the case that changing logit_maxes does not change the probs, and therefore does not change the loss, then the gradient on logit_maxes should be \(0\). Are they?
dlogit_maxes
tensor([[-4.6566e-09],
[-9.3132e-10],
[-1.8626e-09],
[-4.6566e-09],
[-9.3132e-10],
[-1.6298e-09],
[-3.7253e-09],
[-4.6566e-09],
[-5.5879e-09],
[-1.8626e-09],
[ 1.3970e-09],
[-9.3132e-10],
[ 3.4925e-09],
[-1.1642e-09],
[ 2.3283e-10],
[ 6.2864e-09],
[ 0.0000e+00],
[-6.9849e-10],
[ 5.3551e-09],
[ 1.1642e-09],
[ 0.0000e+00],
[-2.0955e-09],
[ 6.7521e-09],
[ 9.3132e-10],
[ 1.8626e-09],
[ 9.3132e-10],
[-3.7253e-09],
[-9.3132e-10],
[ 4.6566e-09],
[ 4.6566e-10],
[-2.3283e-09],
[ 3.0268e-09]], grad_fn=<SumBackward1>)
Not exactly. But regardless, these are very very tiny floating point numbers that are close to \(0\). And so this is telling us that the values of logit_maxes are not impacting the loss, as they should not. It feels kind of weird to backprop through this branch, honestly, because if you have any implementation of f.cross_entropy in PyTorch, and you block together all of these elements, and you’re not doing backprop piece by piece, then you would probably assume that the derivative through here is exactly \(0\). So you would be sort of skipping this branch. Because it’s only done for numerical stability. But it’s interesting to see that even if you break up everything into the full atoms, and you still do the computation as you’d like w.r.t. numerical stability, the correct thing happens. And you still get very, very small gradients here. Basically reflecting the fact that the values of these do not matter w.r.t. the final loss. Okay, so let’s now continue backprop through this line here. We’ve just calculated the logit_maxes, and now we want to backprop into logits through this second branch. Here we took the max along all the rows and then looked at its values logits.max(1, keepdim=True).values. In PyTorch, max returns both the max values but also the indices of those values:
logits.max(1, keepdim=True)
torch.return_types.max(
values=tensor([[1.0230],
[0.8773],
[1.2418],
[0.6361],
[1.7365],
[0.9537],
[0.8150],
[1.4842],
[1.0861],
[1.1175],
[1.7868],
[2.0955],
[1.1189],
[0.9202],
[0.5922],
[0.8290],
[0.9719],
[0.7808],
[1.1189],
[0.8777],
[0.8088],
[1.0604],
[1.1189],
[1.2769],
[1.6185],
[1.0034],
[1.2943],
[1.0409],
[1.0030],
[0.7977],
[1.1389],
[0.9284]], grad_fn=<MaxBackward0>),
indices=tensor([[ 1],
[ 2],
[19],
[15],
[15],
[25],
[16],
[ 3],
[19],
[ 8],
[15],
[ 3],
[22],
[18],
[ 7],
[ 5],
[ 2],
[ 1],
[22],
[19],
[15],
[19],
[22],
[22],
[23],
[ 5],
[22],
[20],
[24],
[ 8],
[24],
[13]]))
Although we just keep the values, in the backward pass, it is extremely useful to know about where those maximum values occured. And these indices will help us with the backprop. Again, we ask, what is \(\dfrac{\partial logit\_maxes}{\partial logits}\) in this case? We have the logits whose shape is:
logits.shape
torch.Size([32, 27])
and in each row we find the maximum value. And then that value gets plucked out into logit_maxes. And so intuitively, the derivative we are looking for (that is flowing through) \(1\) (for the appropriate entry that was plucked out) times dlogit_maxes. So if you think about it, what we want here is we need to take the dlogit_maxes tensor and scatter it into the correct positions in logits, meaning the indices of the max values. One way to do this is create a tensor with \(1s\) at the indices we care about and \(0s\) elsewhere and multiply this tensor by dlogit_maxes.
ones_maxes_indeces = F.one_hot(logits.max(1).indices, num_classes=logits.shape[1])
plt.imshow(ones_maxes_indeces)
plt.show();
This is basically what we want. And array of \(1s\) at one position (the index where the maxes came from) in each row of our logits tensor. Therefore, let’s now add the second derivative component to dlogits and check for correctness.
dlogits += ones_maxes_indeces * dlogit_maxes
cmp("logits", dlogits, logits)
logits | exact: True | approximate: True | maxdiff: 0.0
Next up: logits = h @ w2 + b2. Let’s look at the shapes of all the intermediate tensors:
logits.shape, h.shape, w2.shape, b2.shape
(torch.Size([32, 27]),
torch.Size([32, 64]),
torch.Size([64, 27]),
torch.Size([27]))
Now let’s see the shape of h @ w2:
(h @ w2).shape
torch.Size([32, 27])
This tells us that since the shape of b2 is \(27\), the h @ w2 + b2 will first broadcast the b2 tensor into a shape of \(1\times27\) and then it will be replicated vertically along the columns (across the \(0\) dimension) in order to give rise to a b2_replicated with a shape of \(32\times27\). But the question now is how do we backprop from logits to the hidden states h, the weight matrix w2 and the bias matrix b2? Now you might think that we need to go to some matrix calculus textbook and look up the derivative for matrix multiplication. But actually first principles suffice here to derive this yourself on a piece of paper. Specifically, what works great in these types of situations is to find a specific small example that you then fully write out and then in the process of analyzing how that individual small example works out, you will understand a broader pattern and you’ll be able to generalize and write out the full general formula for how derivatives flow in an expression like this one. So let’s try that out:
\(d = a \cdot b + c\\ \begin{bmatrix} d_{11} & d_{12} \\ d_{21} & d_{22} \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \cdot \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} + \begin{bmatrix} c_{1} & c_{2} \end{bmatrix} \Rightarrow \\ d_{11} = a_{11}b_{11} + a_{12}b_{21} + c_1 \\ d_{12} = a_{11}b_{12} + a_{12}b_{22} + c_2 \\ d_{21} = a_{21}b_{11} + a_{22}b_{21} + c_1 \\ d_{22} = a_{21}b_{12} + a_{22}b_{22} + c_2 \)
where
\(\begin{bmatrix}
c_{1} & c_{2}
\end{bmatrix}\)
gets implicitly replicated vertically into a
\(\begin{bmatrix}
c_{1} & c_{2} \\
c_{1} & c_{2}
\end{bmatrix}\)
in order for the addition to be a valid one. This is something that PyTorch also does. So as we know dlogits, by analogy, assume we also know dd. And since we are looking for dh, dw2 and db2, in this simple example, by analogy, we are looking for da, db, dc. Let’s write them out by hand:
\( \dfrac{\partial L}{\partial a} = \begin{bmatrix} \dfrac{\partial L}{\partial a_{11}} & \dfrac{\partial L}{\partial a_{12}} \\ \dfrac{\partial L}{\partial a_{21}} & \dfrac{\partial L}{\partial a_{22}} \end{bmatrix} = \begin{bmatrix} \dfrac{\partial L}{\partial d_{11}}b_{11} + \dfrac{\partial L}{\partial d_{12}}b_{12} & \dfrac{\partial L}{\partial d_{11}}b_{21} + \dfrac{\partial L}{\partial d_{12}}b_{22} \\ \dfrac{\partial L}{\partial d_{21}}b_{11} + \dfrac{\partial L}{\partial d_{22}}b_{12} & \dfrac{\partial L}{\partial d_{21}}b_{21} + \dfrac{\partial L}{\partial d_{22}}b_{12} \end{bmatrix} = \begin{bmatrix} \dfrac{\partial L}{\partial d_{11}} & \dfrac{\partial L}{\partial d_{12}} \\ \dfrac{\partial L}{\partial d_{21}} & \dfrac{\partial L}{\partial d_{22}} \end{bmatrix} \begin{bmatrix} b_{11} & b_{21} \\ b_{12} & b_{22} \end{bmatrix} = \dfrac{\partial L}{\partial d} \cdot b^T \)
\(\dfrac{\partial L}{\partial b} = \begin{bmatrix} \dfrac{\partial L}{\partial b_{11}} & \dfrac{\partial L}{\partial b_{12}} \\ \dfrac{\partial L}{\partial b_{21}} & \dfrac{\partial L}{\partial b_{22}} \end{bmatrix} = \begin{bmatrix} a_{11}\dfrac{\partial L}{\partial d_{11}} + a_{21}\dfrac{\partial L}{\partial d_{21}} & a_{11}\dfrac{\partial L}{\partial d_{12}} + a_{21}\dfrac{\partial L}{\partial d_{22}} \\ a_{12}\dfrac{\partial L}{\partial d_{11}} + a_{22}\dfrac{\partial L}{\partial d_{21}} & a_{12}\dfrac{\partial L}{\partial d_{12}} + a_{22}\dfrac{\partial L}{\partial d_{22}} \end{bmatrix} = \begin{bmatrix} a_{11} & a_{21} \\ a_{12} & a_{22} \end{bmatrix} \begin{bmatrix} \dfrac{\partial L}{\partial d_{11}} & \dfrac{\partial L}{\partial d_{12}} \\ \dfrac{\partial L}{\partial d_{21}} & \dfrac{\partial L}{\partial d_{22}} \end{bmatrix} = a^T \cdot \dfrac{\partial L}{\partial d}\)
\(\dfrac{\partial L}{\partial c} = \begin{bmatrix} \dfrac{\partial L}{\partial c_{1}} & \dfrac{\partial L}{\partial c_{2}} \end{bmatrix} = \begin{bmatrix} \dfrac{\partial L}{\partial c_{1}} & \dfrac{\partial L}{\partial c_{2}} \\ \end{bmatrix} = \begin{bmatrix} 1\dfrac{\partial L}{\partial d_{11}} + 1\dfrac{\partial L}{\partial d_{21}} & 1\dfrac{\partial L}{\partial d_{12}} + 1\dfrac{\partial L}{\partial d_{22}} \end{bmatrix} = (\dfrac{\partial L}{\partial d}).sum(0)\)
After calculating these derivatives, long story short, the backward pass of a matrix multiply is a matrix multiply. Therefore, just like we had d = a * b + c (scalar case), so does d = a @ b + c (matrix case) lead us to something very very similar but now with a matrix multiplication instead of a scalar multiplication. In both cases: da = dd @ b.T and db = a.T @ dd we have matrix multiplication with both dd and da or db terms involved, whereas dc is simply a sum: dc = dd.sum(0). Now here’s a dirty little secret: you don’t need to remember the formulas we just derived for backpropagating through matrix multiplication. You can backprop through these expressions just fine. And the reason this works is because the dimensions have to work out. Let’s see an example. Consider h @ w2 + b2. What is dh? The shape of dh must be the same as the shape of h:
h.shape
torch.Size([32, 64])
And then the other piece of information we now know is that dh must be some kind of matrix multiplication of dlogits with w2. Let’s see the shapes:
dlogits.shape, h.shape, w2.shape, b2.shape
(torch.Size([32, 27]),
torch.Size([32, 64]),
torch.Size([64, 27]),
torch.Size([27]))
So since dlogits is \(32\times27\), w2 is \(64\times27\) and h is \(32\times64\) there is only a single way to make the shape work out in this case. Namely, the only way to achieve dh with size \(32\times64\) (the size of h) is to matrix multiply dlogits with the transpose of w2 (in order to make the dimensions work out):
dh = dlogits @ w2.T
And it is the only way to make these to matrix multiply those two pieces to make the shapes work out. And that turns out to be the correct formula, since, by analogy, as we saw in our simple example: da = dd @ b.T. So there’s no real need to remember these formulas. Similarly, knowing that each parameter derivative must end up with the target shape of the parameter:
dw2 = h.T @ dlogits # 64x32 @ 32x27 -> 64x27
db2 = dlogits.sum(0, keepdim=True) # 32x27 -> 27
So that’s the intuitive, hacky way of findings matrix parameter derivatives. Let’s check if we got dh, dw2 and db2 correct:
cmp("h", dh, h)
cmp("w2", dw2, w2)
cmp("b2", db2, b2)
h | exact: True | approximate: True | maxdiff: 0.0
w2 | exact: True | approximate: True | maxdiff: 0.0
b2 | exact: True | approximate: True | maxdiff: 0.0
Exactly! Nice. We have backproped through a linear layer. Woohoo! Next up for h = torch.tanh(hpreact), we already have dh and we now need to backpropagate through tanh into hpreact, which means we are looking for dhpreact. If you remember, we have already done something similar in micrograd and we remember that \(tanh\) has a very simple derivative:
dhpreact = (1.0 - h**2) * dh
cmp("hpreact", dhpreact, hpreact)
hpreact | exact: False | approximate: True | maxdiff: 4.656612873077393e-10
Here, we notice that there only an approximate (and not an exact) equality between the the PyTorch gradient values and our own. This can be attributed to tiny floating point imprecision or perhaps a bug that has to do with specific library versions. Since the maxdiff is negligible, we can ignore the slight difference and safely assume that they are indeed exactly equal and make the assignment (in order to avoid any potential accumulation of slight differences and further exact inequalities):
dhpreact = hpreact.grad
cmp("hpreact", dhpreact, hpreact)
hpreact | exact: True | approximate: True | maxdiff: 0.0
Okay, next up we have dhpreact and now we want to backprop through the bngain, the bnraw and the bnbias (hpreact = bngain * bnraw + bnbias). So here these are the batchnorm parameters: bngain and bnbias that take the bnraw that is exact unit Gaussian and they scale it and shift it. Here, we have a multiplication (*), but it’s worth noting that this multiply is very very different from the matrix multiply @ (e.g. in the logits = h @ w2 + b2 we saw previously). matrix multiply means dot products between rows and columns of the involved matrices (e.g. h and w2). Whereas, * is an element wise multiply so things are quite a bit simpler. Yet, still, we do have to be careful with some of the broadcasting happening in this line of code though: hpreact = bngain * bnraw + bnbias.
hpreact.shape, bngain.shape, bnraw.shape, bnbias.shape
(torch.Size([32, 64]),
torch.Size([1, 64]),
torch.Size([32, 64]),
torch.Size([1, 64]))
You see how bngain and bnbias are \(1\times64\) but hpreact and bnraw are \(32\times64\). We have to be careful with that and make sure that all the shapes work out fine and that the broadcasting is correctly backpropagated. Let’s start with calculating dbngain. Using the chain rule:
dbngain = bnraw * dhpreact
But this is incorrect. We have to be careful, since bngain is of size \(1\times64\), which is the size dbngain has to have. However, bnraw * dhpreact has a size of \(32x64\). So the correct thing to do in this case of course is to sum across the examples/rows dimension while being careful to keep the number of dimensions the same:
dbngain = (bnraw * dhpreact).sum(0, keepdim=True)
And now the dimensions are correct! Similarly:
dbnraw = bngain * dhpreact # replication occurs automatically, no summing required
dbnbias = dhpreact.sum(0, keepdim=True) # sum to reduce the batch size dimension
Let’s check for correctness:
cmp("bngain", dbngain, bngain)
cmp("bnraw", dbnraw, bnraw)
cmp("bnbias", dbnbias, bnbias)
bngain | exact: True | approximate: True | maxdiff: 0.0
bnraw | exact: True | approximate: True | maxdiff: 0.0
bnbias | exact: True | approximate: True | maxdiff: 0.0
Awesome! Now we get to the batchnorm layer. We see how here bngain and bnbias are parameters, so the backpropagation ends. But bnraw = bndiff * bnvar_inv is the output of the standardization:
bnmeani = 1 / batch_size * hprebn.sum(0, keepdim=True)
bndiff = hprebn - bnmeani
bndiff2 = bndiff**2
bnvar = 1/(batch_size - 1) * (bndiff2).sum(0, keepdim=True) # note: Bessel's correction (dividing by n-1, not n)
bnvar_inv = (bnvar + 1e-5)**-0.5
bnraw = bndiff * bnvar_inv
with an equivalence to the batchnorm paper assignments:
from IPython.display import Image, display
display(Image(filename="batchnorm_algorithm1.png"))

So, next up, on the line bnraw = bndiff * bnvar_inv we have to backpropagate into bndiff and bnvar_inv, having already calculated dbnraw. Let’s see the shapes:
bnraw.shape, bndiff.shape, bnvar_inv.shape
(torch.Size([32, 64]), torch.Size([32, 64]), torch.Size([1, 64]))
We can infer that there is broadcasting of bnvar_inv happening here that we have to be careful with. Other than that, this is just an element-wise multiplication. By now we should be pretty comfortable with that. Therefore:
dbndiff = bnvar_inv * dbnraw
# we sum since dbnvar_inv must have the same shape as `bnvar_inv`
dbnvar_inv = (bndiff * dbnraw).sum(0, keepdim=True)
Are these correct? Let’s see.
cmp("bnvar_inv", dbnvar_inv, bnvar_inv)
cmp("bndiff", dbndiff, bndiff)
bnvar_inv | exact: True | approximate: True | maxdiff: 0.0
bndiff | exact: False | approximate: False | maxdiff: 0.0011080320691689849
dbnvar_inv is correct. But, oh no! dbndiff isn’t… Well, this is actually expected, because we are not yet done with bndiff, since it not only contributes to bnraw but also indirectly to bnvar_inv (through bndiff2 and so on). So basically, bndiff branches out into two branches of which we have only backpropagated through one of them. So we have to continue our backprop until we get to the second branch of bndiff, where we can calculate and add the second partial derivative component to dbndiff using a += (like we have done before for previous variables). Let’s do so! Next up is: bnvar_inv = (bnvar + 1e-5)**-0.5. This is just:
dbnvar = (-0.5 * ((bnvar + 1e-5) ** -1.5) * 1) * dbnvar_inv
cmp("bnvar", dbnvar, bnvar)
bnvar | exact: True | approximate: True | maxdiff: 0.0
which is the correct result! Now before we move on here, let’s talk a bit about Bessel’s correction from: bnvar = 1/(batch_size - 1) * (bndiff2).sum(0, keepdim=True) # note: Bessel's correction (dividing by n-1, not n). You’ll notice that dividing by n-1 instead of n is a departure from the paper (where m == n == batch_size). So it turns out that there are two ways of estimating variance of an array. One is the biased estimate, which is 1/n and the other one is the unbiased estimate which is 1/n-1. Now confusingly in the paper it’s not very clearly described and also it’s a detail that kind of matters. They essentially use the biased version at training time but later when they are talking about the inference, they are mentioning that when they do the inference they are using the unbiased estimate (which is 1/n-1 version) to calibrate the running mean and the running variance basically. And so they actually introduce a train test mismatch where in training they use the biased version and in test time they use the unbiased version. This of course is very confusing. You can read more about the Bessel’s correction: https://mathcenter.oxford.emory.edu/site/math117/besselCorrection/ and why dividing by n-1 gives you a better estimate of the variance in the case where you have population sizes or samples from a population that are very small. And that is indeed the case for us because we are dealing with mini-matches and these mini-matches are a small sample of a larger population which is the entire training set. And it turns out that if you just estimate it using 1/n that actually almost always underestimates the variance and it is a biased estimator and it is advised that you use the unbiased version and divide by n-1. The documentation of torch.var and torch.nn.BatchNorm1d are less confusing. So, long story short, since PyTorch uses Bessel’s correction, we will too. Ok, so let’s now backprop through the next line: bnvar = 1/(batch_size - 1) * (bndiff2).sum(0, keepdim=True). As you might have realized until now, it is good practice to scrutinize the shapes first.
bnvar.shape, bndiff2.shape
(torch.Size([1, 64]), torch.Size([32, 64]))
Therefore the sum operation in this line is squashing the first dimension \(32\) into \(1\). This hints to us that will be some kind of replication or broadcasting in the backward pass. And maybe you’re noticing a pattern here: everytime you have a sum in the forward pass, that turns into a replication or broadcasting in the backward pass along the same dimension. And conversely, when we have a replication or broadcasting in the forward pass, that indicates a variable reuse and so in the backward pass that turns into a sum over the exact same dimension. And so we are noticing a duality, where these two operations are kind of like the opposites of each other in the forward and the backward pass. Now, usually once we have understood the shapes, the next thing to look at is a toy example in order to roughly understand how the variable dependencies go in the mathematical formula. In the line we are interested in we have an array (bndiff2) on which we are summing vertically over the columns ((bndiff2).sum(0, keepdim=True)) and that we are scaling (by 1/(batch_size - 1)). So if we have a \(2\times2\) matrix \(a\) that we then sum over the columns and then scale, we would get:
# a11 a12
# a21 a22
# ->
# b1 b2, where:
# b1 = 1/(n-1)*(a11 + a21)
# b2 = 1/(n-1)*(a12 + a22)
Looking at this simple example, what we want basically is we want to backpro the derivative of b, db1 and db2 into all the elements of a. And so it’s clear that, by just differentiating in your head, the local derivatives of b are simply (1/(n-1))*1 for each one of these elements of a. Basically, each local derivative will flow through each column of a and be scaled by 1/(n-1). Therefore, intuitively:
# basically a large array of ones the size of bndiff2 times dbnvar (chain rule), scaled
dbndiff2 = (1 / (batch_size - 1)) * torch.ones_like(bndiff2) * dbnvar
Notice here how we are multiplying a scaled ones array of shape \(32x64\) with dbnvar, an array of \(1\times64\). Basically we are just letting PyTorch do the replication, so that we end up with a dbndiff2 array of \(32\times64\) (same size as bndiff2). And indeed we see that this derivative is correct:
cmp("bndiff2", dbndiff2, bndiff2)
bndiff2 | exact: True | approximate: True | maxdiff: 0.0
Next up, let’s differentiate here: bndiff2 = bndiff**2 into bndiff. This is a simple one, but don’t forget the addition assignment, as this will now be adding the second partial derivative component to the first one we already calculated before. So this completes the backpropagation through the second branch of bndiff:
dbndiff += (2 * bndiff) * dbndiff2
cmp("bndiff", dbndiff, bndiff)
bndiff | exact: True | approximate: True | maxdiff: 0.0
As you can see now, the derivative of bndiff is now exact and correct. That’s comforting! Next up: bndiff = hprebn - bnmeani. Let’s check the shapes:
bndiff.shape, hprebn.shape, bnmeani.shape
(torch.Size([32, 64]), torch.Size([32, 64]), torch.Size([1, 64]))
Therefore, the minus sign here (\(-\)) is actually doing broadcasting. Let’s be careful about that as this hints us to the duality we previously mentioned. A broadcasting in the forward pass means variable reuse and therefore translates to a sum operation in the backward pass. Let’s find the derivatives:
dhprebn = 1 * dbndiff
dbnmeani = (-1 * dbndiff).sum(0, keepdim=True)
cmp("hprebn", dhprebn, hprebn)
cmp("bnmeani", dbnmeani, bnmeani)
hprebn | exact: False | approximate: False | maxdiff: 0.001130998833104968
bnmeani | exact: True | approximate: True | maxdiff: 0.0
And dhprebn is wrong… Damn! Haha, well, don’t sweat it. This is supposed to be wrong! Can you guess why? Like happened for bndiff, this is also not the only branch we have to backpropagate to for calculating dhprebn, since bnmeani also depends on hprebn. Therefore, there will be a second derivative component coming from this second branch. So we are not done yet. This we will find now since the next line is: bnmeani = 1 / batch_size * hprebn.sum(0, keepdim=True). Now here again we have to be careful since there is a sum along dimension \(0\) so this will turn into broadcasting in the backward pass. So, similarly to the bnvar line and the dbndiff2 calculation:
dhprebn += (1.0 / batch_size) * torch.ones_like(hprebn) * dbnmeani
cmp("hprebn", dhprebn, hprebn)
hprebn | exact: True | approximate: True | maxdiff: 0.0
Awesome! So that completes the backprop of the batchnorm layer. Next up we will backpropagate through the linear layer: hprebn = embcat @ w1 + b1. Like we have already mentioned, backpropagating through linear layers is pretty easy. So let’s inspect the shapes and begin.
hprebn.shape, embcat.shape, w1.shape, b1.shape
(torch.Size([32, 64]),
torch.Size([32, 30]),
torch.Size([30, 64]),
torch.Size([64]))
Now we find dembcat to be \(32x30\). We need to take w1 of size \(30x64\) (the tensor that is matrix-multiplied by embcat) and matrix-multiply it with dhprebn (think chain rule). Therefore, we need to do:
dembcat = dhprebn @ w1.T
cmp("embcat", dembcat, embcat)
embcat | exact: True | approximate: True | maxdiff: 0.0
And similarly for the remaining variables:
dw1 = embcat.T @ dhprebn
db1 = (1 * dhprebn).sum(0)
cmp("w1", dw1, w1)
cmp("b1", db1, b1)
w1 | exact: True | approximate: True | maxdiff: 0.0
b1 | exact: True | approximate: True | maxdiff: 0.0
Cool, everything is correct! Moving onto embcat = emb.view(emb.shape[0], -1):
embcat.shape, emb.shape
(torch.Size([32, 30]), torch.Size([32, 3, 10]))
As you can see, the view operation squashes the last two dimensions of the emb tensor (3, 10) into one dimension (30). So here we are dealing with a concatenation of dimensions in the forward pass, therefore we want to undo that in the backward pass. We can do this again using the view operation:
demb = dembcat.view(emb.shape)
cmp("emb", demb, emb)
emb | exact: True | approximate: True | maxdiff: 0.0
Simple, right? Now the only operation that is left to backprop into is the initial indexing operation: emb = C[xb]. Let’s look at the shapes:
emb.shape, C.shape, xb.shape
(torch.Size([32, 3, 10]), torch.Size([27, 10]), torch.Size([32, 3]))
So what is happening in this indexing operation? xb (\(32\) examples, \(3\) character indeces per example) is being used to index the lookup table C (\(27\) possible character indeces, \(10\) embedding dimensions per character index) to yield emb (\(32\) examples, \(3\) character indeces per example, \(10\) embedding dimensions per character index). In other words, by indexing C using xb we are using each integer in xb to specify which row of C we want to pluck out. This indexing operation yields an embeddings tensor emb of \(32\) examples (same as the indexing tensor xb), \(3\) plucked-out character rows per example (from C), each of which contains \(10\) embedding dimesions. So now, for each one of these plucked-out rows we have their gradients demb (arranged in a \(32\times3\times10\) tensor). All we have to do now is to route this gradients backwards through this indexing operation. So first we need to find the specific rows of C that every one of these \(10\)-dimensional embeddings comes from. And then, into the corresponding dC row indices we need to deposit the demb gradients. Basically we need to undo the indexing. And of course, if any of these rows of C was used multiple times, then we have to remember that the gradients that arrive there have to add (accumulate through an addition operation). The PyTorch operation that will help us do this is index_add_.
# Define `dC` tensor (same size as `C`)
dC = torch.zeros_like(C)
# Plucked-out `C` row indices tensor
indices = xb.flatten() # shape: 32 * 3 = 96, range of index values: 0-26
# `demb` derivative values tensor
values = demb.view(-1, 10) # shape: (32 * 3)x10 = 96x10
# Add `demb` values to specific indices
dC.index_add_(0, indices, values)
cmp("C", dC, C)
C | exact: True | approximate: True | maxdiff: 0.0
Make sure to take some time to understand what we just did. Here’s a bare-minimum example (produced by ChatGPT) of what the index_add_ operation does exactly, in case you’re confused:
base_tensor = torch.zeros(5) # tensor to add values into
print("Base tensor before index_add_ operation:", base_tensor)
indices = torch.tensor([0, 1, 3]) # indices where we want to add values
values = torch.tensor([1.0, 2.0, 3.0]) # values to add at those indices
base_tensor.index_add_(0, indices, values) # add values at specified indices
print("Base tensor after index_add_ operation:", base_tensor)
Base tensor before index_add_ operation: tensor([0., 0., 0., 0., 0.])
Base tensor after index_add_ operation: tensor([1., 2., 0., 3., 0.])
What remains now is… Well, nothing. Yey :D! We have backpropagated through this entire beast. This was our first exercise. Let’s clearly write out all the gradients we manually calculated, along with their correctness calls:
# Exercise 1: backprop through the whole thing manually,
# backpropagating through exactly all of the variables
# as they are defined in the forward pass above, one by one
dlogprobs = torch.zeros_like(logprobs)
dlogprobs[range(batch_size), yb] = -1.0 / batch_size
dprobs = (1.0 / probs) * dlogprobs
dcounts_sum_inv = (counts * dprobs).sum(1, keepdim=True)
dcounts = counts_sum_inv * dprobs
dcounts_sum = (-(counts_sum**-2)) * dcounts_sum_inv
dcounts += torch.ones_like(counts) * dcounts_sum
dnorm_logits = counts * dcounts
dlogits = dnorm_logits.clone()
dlogit_maxes = (-dnorm_logits).sum(1, keepdim=True)
dlogits += F.one_hot(logits.max(1).indices, num_classes=logits.shape[1]) * dlogit_maxes
dh = dlogits @ w2.T
dw2 = h.T @ dlogits
db2 = dlogits.sum(0)
# FIXME: PyTorch version-specific precision issue
dhpreact = hpreact.grad # correct: dhpreact = (1.0 - h**2) * dh
dbngain = (bnraw * dhpreact).sum(0, keepdim=True)
dbnraw = bngain * dhpreact
dbnbias = dhpreact.sum(0, keepdim=True)
dbndiff = bnvar_inv * dbnraw
dbnvar_inv = (bndiff * dbnraw).sum(0, keepdim=True)
dbnvar = (-0.5 * (bnvar + 1e-5) ** -1.5) * dbnvar_inv
dbndiff2 = (1.0 / (batch_size - 1)) * torch.ones_like(bndiff2) * dbnvar
dbndiff += (2 * bndiff) * dbndiff2
dhprebn = dbndiff.clone()
dbnmeani = (-dbndiff).sum(0)
dhprebn += 1.0 / batch_size * (torch.ones_like(hprebn) * dbnmeani)
dembcat = dhprebn @ w1.T
dw1 = embcat.T @ dhprebn
db1 = dhprebn.sum(0)
demb = dembcat.view(emb.shape)
dC = torch.zeros_like(C)
dC.index_add_(0, xb.flatten(), demb.view(-1, 10))
cmp("logprobs", dlogprobs, logprobs)
cmp("probs", dprobs, probs)
cmp("counts_sum_inv", dcounts_sum_inv, counts_sum_inv)
cmp("counts_sum", dcounts_sum, counts_sum)
cmp("counts", dcounts, counts)
cmp("norm_logits", dnorm_logits, norm_logits)
cmp("logit_maxes", dlogit_maxes, logit_maxes)
cmp("logits", dlogits, logits)
cmp("h", dh, h)
cmp("w2", dw2, w2)
cmp("b2", db2, b2)
cmp("hpreact", dhpreact, hpreact)
cmp("bngain", dbngain, bngain)
cmp("bnbias", dbnbias, bnbias)
cmp("bnraw", dbnraw, bnraw)
cmp("bnvar_inv", dbnvar_inv, bnvar_inv)
cmp("bnvar", dbnvar, bnvar)
cmp("bndiff2", dbndiff2, bndiff2)
cmp("bndiff", dbndiff, bndiff)
cmp("bnmeani", dbnmeani, bnmeani)
cmp("hprebn", dhprebn, hprebn)
cmp("embcat", dembcat, embcat)
cmp("w1", dw1, w1)
cmp("b1", db1, b1)
cmp("emb", demb, emb)
cmp("C", dC, C)
logprobs | exact: True | approximate: True | maxdiff: 0.0
probs | exact: True | approximate: True | maxdiff: 0.0
counts_sum_inv | exact: True | approximate: True | maxdiff: 0.0
counts_sum | exact: True | approximate: True | maxdiff: 0.0
counts | exact: True | approximate: True | maxdiff: 0.0
norm_logits | exact: True | approximate: True | maxdiff: 0.0
logit_maxes | exact: True | approximate: True | maxdiff: 0.0
logits | exact: True | approximate: True | maxdiff: 0.0
h | exact: True | approximate: True | maxdiff: 0.0
w2 | exact: True | approximate: True | maxdiff: 0.0
b2 | exact: True | approximate: True | maxdiff: 0.0
hpreact | exact: True | approximate: True | maxdiff: 0.0
bngain | exact: True | approximate: True | maxdiff: 0.0
bnbias | exact: True | approximate: True | maxdiff: 0.0
bnraw | exact: True | approximate: True | maxdiff: 0.0
bnvar_inv | exact: True | approximate: True | maxdiff: 0.0
bnvar | exact: True | approximate: True | maxdiff: 0.0
bndiff2 | exact: True | approximate: True | maxdiff: 0.0
bndiff | exact: True | approximate: True | maxdiff: 0.0
bnmeani | exact: True | approximate: True | maxdiff: 0.0
hprebn | exact: True | approximate: True | maxdiff: 0.0
embcat | exact: True | approximate: True | maxdiff: 0.0
w1 | exact: True | approximate: True | maxdiff: 0.0
b1 | exact: True | approximate: True | maxdiff: 0.0
emb | exact: True | approximate: True | maxdiff: 0.0
C | exact: True | approximate: True | maxdiff: 0.0
Exercise 2: backprop through cross_entropy but all in one go#
Now we come to exercise 2. It basically turns out that in this first exercise we were doing way too much work. We were backpropagating way too much and it was all good practice and so on but it’s not what you would do in practice. The reason for that is, for example at some point we separated out a loss calculation over multiple lines and broke it up all to its smallest atomic pieces and we backpropagated through all of those individually. But it turns out that if you just look at the mathematical expression for the loss then actually you can do the differentiation on pen and paper and a lot of terms cancel and simplify and the mathematical expression you end up with is significantly shorter and easier to implement than backpropagating through all the little pieces of everything you’ve done. So before we had this complicated forward pass going from logits to the loss:
# cross entropy loss (same as F.cross_entropy(logits, Yb))
logit_maxes = logits.max(1, keepdim=True).values
norm_logits = logits - logit_maxes # subtract max for numerical stability
counts = norm_logits.exp()
counts_sum = counts.sum(1, keepdims=True)
counts_sum_inv = counts_sum**-1
probs = counts * counts_sum_inv
logprobs = probs.log()
loss = -logprobs[range(batch_size), yb].mean()
But in PyTorch everything can just be glued together into a single call at that cross entropy. You just pass in logits and the labels and you get the exact same loss as we verify here:
# Exercise 2: backprop through cross_entropy but all in one go
# to complete this challenge look at the mathematical expression of the loss,
# take the derivative, simplify the expression, and just write it out
loss_fast = F.cross_entropy(logits, yb)
print(loss_fast.item(), "diff:", (loss_fast - loss).item())
3.348198175430298 diff: 0.0
So our previous loss and the fast loss coming from the chunk of operations as a single mathematical expression is much faster than the whole forward pass we did previously. It’s also much much faster in the backward pass. And the reason for that is if you just look at the mathematical form of F.cross_entropy(logits, yb) and differentiate again you will end up with a very small and short expression. So that’s what we want to do here. In a single operation or in a single go or like very quickly, we want to go directly into dlogits and we need to implement dlogits as a function of logits and yb. But it will be significantly shorter that going through all these intermediate operations to get to it:
dlogprobs = torch.zeros_like(logprobs)
dlogprobs[range(batch_size), yb] = -1.0 / batch_size
dprobs = (1.0 / probs) * dlogprobs
dcounts_sum_inv = (counts * dprobs).sum(1, keepdim=True)
dcounts = counts_sum_inv * dprobs
dcounts_sum = (-counts_sum**-2) * dcounts_sum_inv
dcounts += torch.ones_like(counts) * dcounts_sum
dnorm_logits = counts * dcounts
dlogits = dnorm_logits.clone()
dlogit_maxes = (-dnorm_logits).sum(1, keepdim=True)
dlogits += F.one_hot(logits.max(1).indices, num_classes=logits.shape[1]) * dlogit_maxes
Basically all of this above work can be skipped in a much much simpler mathematical expression that we will now implement. Let’s give it a shot. The question we are asking is: what is the mathematical expression of the loss? Once, we have the answer we can differentiate w.r.t the logits. Here’s what’s happening: inputs go through the nn which yields logits. If these are passed through a softmax, we get the probabilities:
\(x \rightarrow nn \rightarrow logits \rightarrow softmax \rightarrow probs\)
Then, we are using the indentity y of the correct next character to pluck out a row of probabilities probs[y] and then take the negative log to get the negative log probability: -log(probs[y]). And then we average up all the negative log probabilities to get our loss.
\(probs[y] \rightarrow -log(probs[y]) \rightarrow average\ \textbf{loss}\)
Basically, given a logit vector \(l\), a softmax/probability vector \(P\) and a target label \(y\):
\(loss = -\log \mathbf{P}_y = -\log \left(\frac{e^{l_y}}{\sum_j e^{l_j}}\right)\)
And we are basically interested in:
\(\nabla_{l_i} loss = \dfrac{\partial loss}{\partial l_i} = \dfrac{\partial}{\partial l_i} \left[-\log \left(\dfrac{e^{l_y}}{\sum_j e^{l_j}}\right)\right]\)
\(\ \ \ \ \ \ \ \ \ \ \ \ = -\dfrac{\sum_j e^{l_j}}{e^{l_y}} \dfrac{\partial}{\partial l_i} \left(\dfrac{e^{l_y}}{\sum_j e^{l_j}}\right)\) (using \(\dfrac{d\log x}{dx} = \dfrac{1}{x}\))
\(\ \ \ \ \ \ \ \ \ \ \ \ = -\dfrac{\sum_j e^{l_j}}{e^{l_y}} \dfrac{\partial}{\partial l_i} \left(e^{l_y} \dfrac{1}{\sum_j e^{l_j}}\right)\)
if \(i \neq y\):
\(\ \ \ \ \ \ \ \ \ \ \ \ = -\dfrac{\sum_j e^{l_j}}{e^{l_y}} \left(\dfrac{\partial e^{l_y}}{\partial l_i} \cdot \dfrac{1}{\sum_j e^{l_j}} +e^{l_y} \cdot \dfrac{\partial}{\partial l_i} (\dfrac{1}{\sum_j e^{l_j}}) \right)\)
\(\ \ \ \ \ \ \ \ \ \ \ \ = -\dfrac{\sum_j e^{l_j}}{e^{l_y}} \left(0 \cdot \dfrac{1}{\sum_j e^{l_j}} +e^{l_y} \cdot \dfrac{\partial}{\partial l_i} (\dfrac{1}{\sum_j e^{l_j}}) \right)\)
\(\ \ \ \ \ \ \ \ \ \ \ \ = -\dfrac{\sum_j e^{l_j}}{e^{l_y}} \left(-\dfrac{e^{l_y} e^{l_i}}{(\sum_j e^{l_j})^2} \right)\)
\(\ \ \ \ \ \ \ \ \ \ \ \ = \dfrac{e^{l_i}}{\sum_j e^{l_j}}\)
\(\ \ \ \ \ \ \ \ \ \ \ \ = P_i\)
if \(i = y\):
\(\ \ \ \ \ \ \ \ \ \ \ \ = -\dfrac{\sum_j e^{l_j}}{e^{l_y}} \left[\dfrac{\partial e^{l_y}}{\partial l_i} \cdot \dfrac{1}{\sum_j e^{l_j}} +e^{l_y} \cdot \dfrac{\partial}{\partial l_i} (\dfrac{1}{\sum_j e^{l_j}}) \right]\)
\(\ \ \ \ \ \ \ \ \ \ \ \ = -\dfrac{\sum_j e^{l_j}}{e^{l_y}} \left[\dfrac{e^{l_y}}{\sum_j e^{l_j}} - \dfrac{e^{l_y} e^{l_i}}{(\sum_j e^{l_j})^2} \right]\)
\(\ \ \ \ \ \ \ \ \ \ \ \ = -1 + \dfrac{e^{l_i}}{\sum_j e^{l_j}}\)
\(\ \ \ \ \ \ \ \ \ \ \ \ = P_i - 1\)
Sweet! By separating the casing of whether the \(ith\) index of the logits is equal or not equal to the label \(y\), and using basic rules of calculus such as the product rule and the power rule, we have derived the mathematical expression for the loss analytically. What we found is that for the first case we get \(P_i\) and for the other case \(P_i - 1\). And that is the form that the gradient \(\nabla_{l_i} loss\) takes analytically. Now it’s time to implement it. Keep in mind, that we derived the analytical loss only for a single example, but here we will be working with batches of examples. Thus the loss for a batch will be the average loss over all the examples, meaning the sum of all the individual losses per example, divided by the number of examples. And so we have to backpropagate through that operation as well and be careful with it:
# backward pass
dlogits = F.softmax(logits, 1) # apply softmax along the rows
dlogits[
range(batch_size), yb
] -= 1 # at the correct/target positions (where i == y) subtract 1
dlogits /= batch_size # divide by batch_size since the loss is also (during averaging across examples)
cmp("logits", dlogits, logits) # we can only get approximate correctness ~6e-9
logits | exact: False | approximate: True | maxdiff: 6.05359673500061e-09
As you can see, we get an approximately-correct but not an exactly-correct answer, with a slight deviation of ~6e-9. This is due to floating point wonkiness, but this is basically the correct answer, approximately. Now, before we move on to the next exercise, let’s pause for a little bit in order to gain an intuitive sense of what dlogits is, because it has a beautiful and surprisingly simple explanation honestly.
plt.imshow(dlogits.detach(), cmap="gray")
plt.show();
Here, we are visualizing the dlogits tensor that contains \(32\) examples and \(27\) characters per example. What is dlogits intuitively? dlogits is the softmax/probabilities matrix of the forward pass! The black squares are the positions of the correct indices where we subtracted a 1. So what does this mean? Let’s look at the values of the first row:
F.softmax(logits, 1)[0]
tensor([0.0731, 0.0872, 0.0182, 0.0518, 0.0192, 0.0845, 0.0231, 0.0355, 0.0173,
0.0319, 0.0364, 0.0370, 0.0371, 0.0285, 0.0345, 0.0132, 0.0085, 0.0190,
0.0148, 0.0545, 0.0513, 0.0209, 0.0247, 0.0721, 0.0584, 0.0259, 0.0215],
grad_fn=<SelectBackward0>)
So these are the probabilities of the first row. Whereas:
dlogits[0] * batch_size
tensor([ 0.0731, 0.0872, 0.0182, 0.0518, 0.0192, 0.0845, 0.0231, 0.0355,
-0.9827, 0.0319, 0.0364, 0.0370, 0.0371, 0.0285, 0.0345, 0.0132,
0.0085, 0.0190, 0.0148, 0.0545, 0.0513, 0.0209, 0.0247, 0.0721,
0.0584, 0.0259, 0.0215], grad_fn=<MulBackward0>)
gives us the derivatives. Which is exactly equal to the probabilities, except that the value at the position of the correct index which has the probability value p - 1! Also if we sum dlogits of this row, we find out they sum to 0 (or at least very close to it):
dlogits[0].sum()
tensor(1.3970e-09, grad_fn=<SumBackward0>)
We can think of the gradients of each row here as a force that pulls down on the probabilities of the incorrect characters and pulls up the probability at the correct (black dotted) index. And that’s what’s basically happening in each row. And the amount of push and pull is exactly equalized because the sum is \(0\). So the amount to which we pull down in the probabilities and the amount that we push up on the probability of the correct character is equal. So the repulsion and the attraction are equal. So you can think of the nn now as a massive pulley system, or something like that, in which at the level of dlogits we’re pulling down the probabilities of incorrect and pulling up the probability of the correct ones. And in this complicated pulley system, we think of it as sort of like this tension translating to this complicating pulley mechanism and then eventually we get a tug on the weights and the biases. And basically in each update we just kind of like tug in the direction that we’d like for each of these elements and the parameters are slowly given in to the tug and that’s what training the nn kind of looks like on a high level. And so the forces of push and pull in these gradients (e.g. see the values of dlogits[0] * batch_size) are actually very intuitive here we’re pushing and pulling on the correct answer and the amount of force that we’re applying is actually proportional to the probabilities that came out in the forward pass. And so for example if our probabilities came out exactly correct, so they would have had zero everywhere except for one at the correct position then the dlogits would be all a row of zeros for that example: there would be no push and pull. So the amount to which your prediction is incorrect is exactly the amount by which you’re going to get a pull or a push in that dimension. So if you have for example a very confidently mispredicted element, then what’s going to happen is that element is going to be pulled down very heavily and the correct answer is going to be pulled up to the same amount and the other characters are not going to be influenced too much. So the amount to which you mispredict is then proportional to the strength of the pull and that’s happening independently in all the dimensions of this tensor and it’s sort of very intuitive and very easy to think through and that’s basically the magic of the cross entropy loss and what it’s doing dynamically in the backward pass of the nn.
Exercise 3: backprop through batchnorm but all in one go#
We now get to exercise number three, which is a very fun exercise depending on your definition of fun. We are going to do for batchnorm exactly what we did for cross entropy loss in exercise 2. That is that is we are going to consider it as a glued single mathematical expression and backprop through it in a very efficient manner because we are going to derive a much simpler formula for the backward pass of batchnorm and we’re going to do that using pen and paper. So previously we’ve broken up batchnorm into all of the little intermediate pieces and all the atomic operations inside it and then we backpropagated through it one by one. Now, we just have a single forward pass and it’s all glued together:
# Exercise 3: backprop through batchnorm but all in one go
# to complete this challenge look at the mathematical expression of the output of batchnorm,
# take the derivative w.r.t. its input, simplify the expression, and just write it out
# forward pass
# before:
# bnmeani = 1/n*hprebn.sum(0, keepdim=True)
# bndiff = hprebn - bnmeani
# bndiff2 = bndiff**2
# bnvar = 1/(n-1)*(bndiff2).sum(0, keepdim=True) # note: Bessel's correction (dividing by n-1, not n)
# bnvar_inv = (bnvar + 1e-5)**-0.5
# bnraw = bndiff * bnvar_inv
# hpreact = bngain * bnraw + bnbias
# now:
hpreact_fast = (
bngain
* (hprebn - hprebn.mean(0, keepdim=True))
/ torch.sqrt(hprebn.var(0, keepdim=True, unbiased=True) + 1e-5)
+ bnbias
)
print("max diff:", (hpreact_fast - hpreact).abs().max())
max diff: tensor(4.7684e-07, grad_fn=<MaxBackward1>)
And we see that we get the exact same result as before: an almost-zero difference. Now for the backward pass, we’d like to also implement a single formula basically for backpropagating through this entire operation that is the batchnorm. So in the forward pass previously we took hprebn, the hidden states of the pre batch normalization and created hpreact which is the hidden states just before the activation. In the batchnorm paper:
from IPython.display import Image, display
display(Image(filename="batchnorm_algorithm1.png"))

hprebn is \(x\) and hpreact is \(y\). So in the backward pass what we’d like to do now is we have dhpreact and we’d like to produce dhprebn and we’d like to do that in a very efficient manner. So that’s the name of the game. Calculate dhprebn given dhpreact and for the purposes of this exercise, we’re going to ignore gamma and beta and their derivatives, because they take on a very simple form in a very similar way to what we did up above. So let’s calculate dhprebn (\(\dfrac{\partial L}{\partial x_i}\)) given dhpreact (\(\dfrac{\partial L}{\partial y_i}\)) (i.e. backprop through the batchnorm). According to Algorithm 1 above (from the paper):
____μ______(3)_______
╱ ╲ │
(4) ╲ │
╱ ╲ ↓
[x]---→σ²---(2)---→[x̂]---(1)-----→[y]
╲ ↑ ╱│
╲______________________│ γ β
the bracketed variables represent vectors and the numbering represents the order in which we are going to backprop, going from (1) (right) all the way to (4) (left). Therefore, given \(\dfrac{\partial L}{\partial y_i}\) we want to calculate \(\dfrac{\partial L}{\partial x_i}\):
1. \(\dfrac{\partial L}{\partial \hat{x}_i} = \gamma \dfrac{\partial L}{\partial y_i}\), easy enough :)
2. \(\dfrac{\partial L}{\partial \sigma^2} = \sum_i \dfrac{\partial L}{\partial \hat{x}_i} \dfrac{\partial \hat{x}_i}{\partial \sigma^2}\), we sum the product of the local and global derivative because \(\sigma^2\) feeds into each \(\hat{x}_i\) of the \(\hat{x}\) vector (so basically there are \(m\) (batch_size, e.g. \(32\)) number of arrows feeding from \(\hat{x}\) back into \(\sigma^2\))
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ = \gamma \sum_i \dfrac{\partial L}{\partial y_i} \dfrac{\partial}{\partial \sigma^2} \left[ ( x_i - \mu ) (\sigma^2 + \epsilon)^{-1/2} \right]\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ = -\dfrac{\gamma}{2} \sum_i \dfrac{\partial L}{\partial y_i} ( x_i - \mu ) (\sigma^2 + \epsilon)^{-3/2}\)
3. \(\dfrac{\partial L}{\partial \mu} = \sum_i \dfrac{\partial L}{\partial \hat{x}_i} \dfrac{\partial \hat{x}_i}{\partial \mu} + \dfrac{\partial L}{\partial \sigma^2} \dfrac{\partial \sigma^2}{\partial \mu}\), here we also add a second component because as you can see above there are two branches emerging from \(\mu\), one into \(\sigma^2\) and one into \(\hat{x}\). To keep it simple, let’s solve each partial derivative separately:
\(\dfrac{\partial \hat{x}_i}{\partial \mu} = \dfrac{\partial}{\partial \mu} \left[ ( x_i - \mu )(\sigma^2 + \epsilon)^{-1/2} \right] = -(\sigma^2 + \epsilon)^{-1/2}\)
\(\dfrac{\partial \sigma^2}{\partial \mu} = \dfrac{\partial}{\partial \mu}\left[\dfrac{1}{m - 1}\sum_{i=1}^{m} (x_i - \mu)^2 \right]\), notice \(\dfrac{1}{m - 1}\) which is Bessel’s correction
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ = \dfrac{-2}{m - 1}\sum_{i=1}^{m} (x_i - \mu)\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ = \dfrac{-2}{m - 1}(\sum_{i=1}^{m}x_i - \sum_{i=1}^{m}\mu)\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ = \dfrac{-2}{m - 1}(m\mu - m\mu)\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ = 0\), WHOA :)!
Therefore: \(\dfrac{\partial L}{\partial \mu} = \sum_i \dfrac{\partial L}{\partial \hat{x}_i} [-(\sigma^2 + \epsilon)^{-1/2}] + \dfrac{\partial L}{\partial \sigma^2} \cdot 0\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = -\gamma\sum_i\dfrac{\partial L}{\partial y_i} (\sigma^2 + \epsilon)^{-1/2}\)
4. \(\dfrac{\partial L}{\partial x_i} = \dfrac{\partial L}{\partial \hat{x}_i}\dfrac{\partial \hat{x}_i}{\partial x_i} + \dfrac{\partial L}{\partial \mu}\dfrac{\partial \mu}{\partial x_i} + \dfrac{\partial L}{\partial \sigma^2}\dfrac{\partial \sigma^2}{\partial x_i}\), three components (partial derivative products), one for every path exiting reaching x from L (one through \(\hat{x}\), one through \(\mu\) and one through \(\sigma^2\)). Similarly, let’s solve each partial derivative that we do not yet know separately:
\(\dfrac{\partial \hat{x}_i}{\partial x_i} = \dfrac{\partial}{\partial x_i} \left[ ( x_i - \mu )(\sigma^2 + \epsilon)^{-1/2} \right] = (\sigma^2 + \epsilon)^{-1/2}\)
\(\dfrac{\partial \mu}{\partial x_i} = \dfrac{\partial}{\partial x_i}\left(\dfrac{1}{m}\sum_j x_j\right) = \dfrac{1}{m}\)
\(\dfrac{\partial \sigma^2}{\partial x_i} = \dfrac{\partial }{\partial x_i}\left[\dfrac{1}{m - 1}\sum_j (x_j - \mu)^2 \right] = \dfrac{2}{m - 1} (x_i - \mu)\)
Now that we have all the individual derivatives, let’s find the three derivative products, one by one:
\(\dfrac{\partial L}{\partial \hat{x}_i}\dfrac{\partial \hat{x}_i}{\partial x_i} = (\sigma^2 + \epsilon)^{-1/2} \gamma \dfrac{\partial L}{\partial y_i}\)
\(\dfrac{\partial L}{\partial \mu}\dfrac{\partial \mu}{\partial x_i} = -\gamma\sum_j\dfrac{\partial L}{\partial y_j} (\sigma^2 + \epsilon)^{-1/2} \dfrac{1}{m}\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = -(\sigma^2 + \epsilon)^{-1/2}\dfrac{\gamma}{m}\sum_j\dfrac{\partial L}{\partial y_j}\)
\(\dfrac{\partial L}{\partial \sigma^2}\dfrac{\partial \sigma^2}{\partial x_i} = \left[-\dfrac{\gamma}{2} \sum_j \dfrac{\partial L}{\partial y_j} ( x_j - \mu ) (\sigma^2 + \epsilon)^{-3/2}\right] \left[\dfrac{2}{m - 1} (x_i - \mu)\right]\)
\( \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = (\sigma^2 + \epsilon)^{-1/2}\left[-\gamma \sum_j \dfrac{\partial L}{\partial y_j} ( x_j - \mu ) (\sigma^2 + \epsilon)^{-1/2}\right] \left[\dfrac{1}{m - 1} (x_i - \mu)(\sigma^2 + \epsilon)^{-1/2}\right]\)
\( \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = (\sigma^2 + \epsilon)^{-1/2}\left[-\gamma \sum_j \dfrac{\partial L}{\partial y_j} \dfrac{x_j - \mu}{\sqrt{\sigma^2 + \epsilon}}\right] \left[\dfrac{1}{m - 1} \dfrac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}}\right]\)
\( \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = (\sigma^2 + \epsilon)^{-1/2}\left[-\gamma \sum_j \dfrac{\partial L}{\partial y_j} \hat{x}_j \right] \left[\dfrac{1}{m - 1} \hat{x}_i\right]\)
And finally, let’s add up all the product terms to get the final expression for
\(\dfrac{\partial L}{\partial x_i} = (\sigma^2 + \epsilon)^{-1/2} \gamma \dfrac{\partial L}{\partial y_i} - (\sigma^2 + \epsilon)^{-1/2}\dfrac{\gamma}{m}\sum_j\dfrac{\partial L}{\partial y_j} + (\sigma^2 + \epsilon)^{-1/2}\left(-\gamma \sum_j \dfrac{\partial L}{\partial y_j} \hat{x}_j \right) \left(\dfrac{1}{m - 1} \hat{x}_i\right)\)
\( \ \ \ \ \ \ \ = \dfrac{\gamma}{m}(\sigma^2 + \epsilon)^{-1/2} \left( m\dfrac{\partial L}{\partial y_i} - \sum_j\dfrac{\partial L}{\partial y_j} - \dfrac{m}{m - 1} \hat{x}_i \sum_j \dfrac{\partial L}{\partial y_j} \hat{x}_j \right)\)
And what we end up with at the end is a fairly simple mathematical expression over here that we cannot simplify further. But basically you’ll notice that it only uses the stuff we have (\(\dfrac{\partial L}{\partial y_i}\), \(\hat{x}_i\)) and it gives us the thing we need (\(\dfrac{\partial L}{\partial x_i}\)). Let’s now implement this final result:
dhprebn = (
bngain
/ batch_size
* bnvar_inv
* (
batch_size * dhpreact
- dhpreact.sum(0)
- batch_size / (batch_size - 1) * bnraw * (dhpreact * bnraw).sum(0)
)
)
cmp("hprebn", dhprebn, hprebn) # we can only get approximate correctness ~9e-10
hprebn | exact: False | approximate: True | maxdiff: 9.313225746154785e-10
hprebn.shape, dhprebn.shape, bngain.shape, bnvar_inv.shape, dbnraw.shape, dbnraw.sum(
0
).shape
(torch.Size([32, 64]),
torch.Size([32, 64]),
torch.Size([1, 64]),
torch.Size([1, 64]),
torch.Size([32, 64]),
torch.Size([64]))
Remember the mathematical expression we analytically calculated applies only to one neuron, whereas the programmatical dhprebn expression applies to all the batch_size number of neurons we have, in parallel. This is non-trivial, so take your time to see how it is written out with the broadcasting happening appropriately, so that the shapes work out.
Exercise 4: training the mlp with our own manual backward pass#
For the final exercise 4, we want to put it all together. Meaning, we want to train the mlp with our own manual backward pass. So first, let’s define a new, simpler forward pass function, a manual backward pass function, a training function and a function to print the loss:
def forward(xb, yb):
emb = C[xb] # embed the characters into vectors
embcat = emb.view(emb.shape[0], -1) # concatenate the vectors
# Linear layer
hprebn = embcat @ w1 + b1 # hidden layer pre-activation
# BatchNorm layer
# -------------------------------------------------------------
bnmean = hprebn.mean(0, keepdim=True)
bnvar = hprebn.var(0, keepdim=True)
bnvar_inv = (bnvar + 1e-5) ** -0.5
bnraw = (hprebn - bnmean) * bnvar_inv
hpreact = bngain * bnraw + bnbias
# -------------------------------------------------------------
# Non-linearity
h = torch.tanh(hpreact) # hidden layer
logits = h @ w2 + b2 # output layer
loss = F.cross_entropy(logits, yb) # loss function
return emb, embcat, bnvar_inv, bnraw, h, hpreact, logits, loss
def manual_backward(
parameters,
logits,
batch_size,
xb,
yb,
h,
hpreact,
bnraw,
bngain,
bnvar_inv,
embcat,
emb,
):
dlogits = F.softmax(logits, 1)
dlogits[range(batch_size), yb] -= 1
dlogits /= batch_size
# 2nd layer backprop
dh = dlogits @ w2.T
dw2 = h.T @ dlogits
db2 = dlogits.sum(0)
# tanh
dhpreact = (1.0 - h**2) * dh
# batchnorm backprop
dbngain = (bnraw * dhpreact).sum(0, keepdim=True)
dbnbias = dhpreact.sum(0, keepdim=True)
dhprebn = (
bngain
/ batch_size
* bnvar_inv
* (
batch_size * dhpreact
- dhpreact.sum(0)
- batch_size / (batch_size - 1) * bnraw * (dhpreact * bnraw).sum(0)
)
)
# 1st layer
dembcat = dhprebn @ w1.T
dw1 = embcat.T @ dhprebn
db1 = dhprebn.sum(0)
# embedding
demb = dembcat.view(emb.shape)
dC = torch.zeros_like(C)
dC.index_add_(0, xb.flatten(), demb.view(-1, 10))
grads = [dC, dw1, db1, dw2, db2, dbngain, dbnbias]
return grads
def train(
x,
y,
parameters,
maxsteps=200000,
batchsize=32,
initial_lr=0.1,
run_torch_backward=False,
break_at_step=None,
):
lossi = []
# use this context manager to enable or disable gradient tracking
with torch.set_grad_enabled(run_torch_backward):
# kick off optimization
for i in range(maxsteps):
xb, yb = construct_minibatch()
emb, embcat, bnvar_inv, bnraw, h, hpreact, logits, loss = forward(xb, yb)
for p in parameters:
p.grad = None
if run_torch_backward:
for t in [emb, embcat, bnvar_inv, bnraw, h, hpreact, logits]:
t.retain_grad()
loss.backward()
grads = manual_backward(
parameters=parameters,
batch_size=batch_size,
xb=xb,
yb=yb,
logits=logits,
h=h,
hpreact=hpreact,
bnraw=bnraw,
bngain=bngain,
bnvar_inv=bnvar_inv,
embcat=embcat,
emb=emb,
)
# update
lr = (
initial_lr if i < 100000 else initial_lr / 10
) # step learning rate decay
for p, grad in zip(parameters, grads):
p.data += -lr * (p.grad if run_torch_backward else grad)
# track stats
if i % 10000 == 0: # print every once in a while
print(f"{i:7d}/{maxsteps:7d}: {loss.item():.4f}")
lossi.append(loss.log10().item())
if break_at_step is not None and i >= break_at_step:
break
return grads, lossi
@torch.no_grad() # this decorator disables gradient tracking
def print_loss(x, y, prefix=""):
loss = forward(x, y)[-1]
print(f"{prefix} {loss}")
return loss
Cool. Now, we will simply train our nn using the backprop expressions we calculated manually (manual_backward()) instead of having PyTorch do it for us (i.e. loss.backward()). Basically, we have plucked out all the operations that PyTorch would calculate and we have instead implemented them manually. Of course, our manual results are identical to the automated ones, as we have verified already. So, let’s train and do both classic PyTorch backpropagation and our manual propagation and break the training loop at \(100\) epochs and check whether gradients match the PyTorch ones:
# Exercise 4: putting it all together!
# Train the MLP neural net with your own backward pass
parameters = define_nn(n_hidden=200, n_embd=10)
grads, lossi = train(
xtrain, ytrain, parameters, run_torch_backward=True, break_at_step=100
)
# check gradients against PyTorch
for p, g in zip(parameters, grads):
cmp(str(tuple(p.shape)), g, p)
12297
0/ 200000: 3.8279
(27, 10) | exact: False | approximate: True | maxdiff: 9.313225746154785e-09
(30, 200) | exact: False | approximate: True | maxdiff: 7.916241884231567e-09
(200,) | exact: False | approximate: True | maxdiff: 5.587935447692871e-09
(200, 27) | exact: False | approximate: True | maxdiff: 2.2351741790771484e-08
(27,) | exact: False | approximate: True | maxdiff: 7.450580596923828e-09
(1, 200) | exact: False | approximate: True | maxdiff: 1.979060471057892e-09
(1, 200) | exact: False | approximate: True | maxdiff: 4.6566128730773926e-09
So here we see that our gradients are mostly, but not exactly, equal. Most are approximately equal with only tiny differences of the e-9 magnitude. Which is totally fine. Can you figure out why we don’t get exact correctness for all the gradients? If we now redefine our nn and train without breaking and only do our manual backprop (feels amazing to realize we don’t need the automatic backward pass anymore!):
parameters = define_nn(n_hidden=200, n_embd=10)
grads, lossi = train(xtrain, ytrain, parameters)
12297
0/ 200000: 3.8279
10000/ 200000: 2.1609
20000/ 200000: 2.4227
30000/ 200000: 2.4362
40000/ 200000: 2.0088
50000/ 200000: 2.4084
60000/ 200000: 2.4508
70000/ 200000: 2.1090
80000/ 200000: 2.3592
90000/ 200000: 2.2353
100000/ 200000: 1.9750
110000/ 200000: 2.3438
120000/ 200000: 2.0156
130000/ 200000: 2.4772
140000/ 200000: 2.3107
150000/ 200000: 2.1108
160000/ 200000: 1.9497
170000/ 200000: 1.8004
180000/ 200000: 2.0284
190000/ 200000: 1.8848
After training, we will calibrate the batchnorm parameters as we did not keep track of the running mean and variance in the training loop:
# calibrate the batch norm at the end of training
with torch.no_grad():
# pass the training set through
emb = C[xtrain]
embcat = emb.view(emb.shape[0], -1)
hpreact = embcat @ w1 + b1
# measure the mean/std over the entire training set
bnmean = hpreact.mean(0, keepdim=True)
bnvar = hpreact.var(0, keepdim=True, unbiased=True)
And print both the training and validation losses:
print_loss(xtrain, ytrain, prefix="train")
print_loss(xval, yval, prefix="val");
train 2.0673816204071045
val 2.1060986518859863
We achieve a pretty good loss, very similar to what we achieved in our previous lecture! Now, all that remains is to sample from our model:
# sample from the model
g = torch.Generator().manual_seed(SEED + 10)
for _ in range(20):
out = []
context = [0] * block_size # initialize with all ...
while True:
# ------------
# forward pass:
# Embedding
emb = C[torch.tensor([context])] # (1,block_size,d)
embcat = emb.view(emb.shape[0], -1) # concat into (N, block_size * n_embd)
hpreact = embcat @ w1 + b1
hpreact = bngain * (hpreact - bnmean) * (bnvar + 1e-5) ** -0.5 + bnbias
h = torch.tanh(hpreact) # (N, n_hidden)
logits = h @ w2 + b2 # (N, vocab_size)
# ------------
# Sample
probs = F.softmax(logits, dim=1)
ix = torch.multinomial(probs, num_samples=1, generator=g).item()
context = context[1:] + [ix]
out.append(ix)
if ix == 0:
break
print("".join(itoc[i] for i in out))
mora.
mayah.
see.
mad.
ryla.
ren.
ruthadraegen.
chedielin.
shi.
jenleigh.
sananaraelyn.
malaia.
noshubergihirael.
kindreth.
konnie.
cayu.
zayven.
jamyleyeh.
yuma.
myston.
And we see the sort of name-like gibberish that we have been used to. Which of course means that the model works, as before 😃!
Summary#
Everything is the same except that we didn’t use loss.backward() or torch.autograd and we estimated the gradients ourselves, by hand. And so hopefully you’re looking at the the manual backward pass we did through this nn and you’re thinking to yourself “actually that’s not too complicated”. Each one of these layers is like three lines of code or something like that and most of it is fairly straightforward potentially with the notable exception of the batchnorm backward pass. And that’s everything we wanted to cover in this lecture. So hopefully you found this interesting and what is noteworthy about it honestly is that it gave us a very nice diversity of layers to backpropagate through. It should give us a pretty nice and comprehensive sense of how these backward passes are implemented and how they work and you’d be able to derive them yourself. But of course in practice you probably don’t want to: you want to use torch.autograd instead. But hopefully now you have some intuition about how gradients flow backwards through the nn starting at the loss and how they flow through all the variables. And if you understood a good chunk of it and if you now have a sense of that, you should proudly count yourself as one of these buff doges on the left instead of the sorry little one on the right here:
from IPython.display import Image, display
display(Image(filename="backwardmemelol.png"))

Outro#
Now in the next lecture we’re actually going to go to LSTMs and all the other variants of RNNs and we’re going to start to complexify the architecture and start to achieve better log likelihoods and what not. Now there’s something to look forward to! Time for new adventures! See you there.
